Question

If the radius of the circle is 5 cm and distance from centre to the point of intersection of two tangents is 13 cm. Find length of the tangent.
A.11 cm
B.10 cm
C.12 cm
D.13 cm

Answer 1

Hint: Here we consider the property i.e..The radius of a circle is perpendicular to its tangent and Pythagoras theorem: Let us consider a triangle $ABC$ whose $\angle B$ is right angle. Then, it states that, $Hypotenuse{e^2} = Bas{e^2} + Perpendicula{r^2}$

Complete step by step answer:

                       ![](https://www.vedantu.com/question-sets/91a0d72b-af61-4f1d-a497-da509d3222ef5481373514707064766.png)  

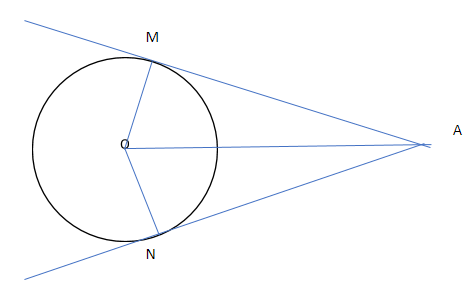
Let us consider, O be the center of the circle. And AM and AN be two tangents which meets at A.
Now according to the problem, $OA = 13$and the radius is $5$cm.
So, $OM = ON = 5$
We have to find the length of the tangent that is to find the length of $AM.$
Let us consider the triangle $AOM$.
We know that the radius of a circle is perpendicular to its tangent.
Then, $OM \bot OA$. So, triangle $AOM$is a right-angle triangle whose, $\angle OMA = {90^ \circ }$.
We can say that, $OM$is the perpendicular, $AM$ is the base and $AO$ is the hypotenuse.
Then by Pythagoras theorem we can further say that,
$A{O^2} = O{M^2} + A{M^2}$
Now let us substitute the values of $OA = 13$ and $OM = 5$ to find AM,
Therefore, we get,
${13^2} = {5^2} + A{M^2}$
Now we are going to solve the above equation to get AM,
$A{M^2} = 169 - 25$
We should solve again to find AM,
$AM = \sqrt {144} = 12$
Hence, the length of the tangent is found to be $12$cm.
The correct option is (C)$12$ cm.

Note-: Here, $AM = \pm \sqrt {144} = \pm 12$
We take only the positive value since the length cannot be negative. Here we can also use the right angle triangle AON to find the length of the tangent.