Question

If the radius of gyration of the body about the axis at a distance $5cm$ from the center of mass is $13cm$ . What will be the radius of gyration about the parallel axis through the center of mass?

Answer 1

To solve this problem, we need to know the parallel axis theorem. The parallel axis theorem states that the Moment of Inertia of an object through an axis can be calculated by using the help of an axis that is parallel to it and passes through the center of mass of the object.

Complete step by step solution:
Step 1:
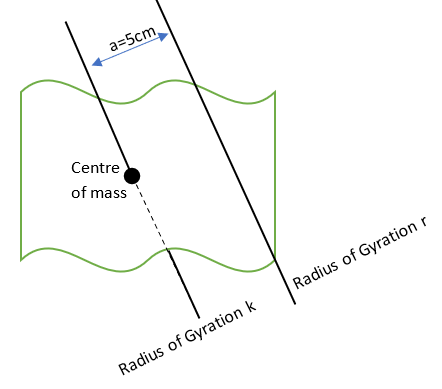
Let us assume that the Radius of Gyration of an axis passing through the center of mass be $k$ while the Radius of Gyration of the given axis passing at a distance of $5cm$ from the center of mass be $r$ .
Let us denote the distance of $5cm$ as a which is the distance between the axes.
Let the mass of the object be $m$
Step 2:
Given that $a = 5cm$
$r = 13cm$

Step 3:
By using parallel axis theorem
$m{r^2} = m{k^2} + m{a^2}$
By substituting the given values in the above equation,
We get
$m \times {13^2} = m \times {k^2} + m \times {5^2}$
As both sides have m, we can remove it and we get simplifies equation as
$\Rightarrow {13^2} = {k^2} + {5^2}$
$\Rightarrow {k^2} = {13^2} - {5^2}$
$\Rightarrow {k^2} = 169 - 25 = 144$
$\Rightarrow k = \sqrt {144}$
$\Rightarrow k = 12$
Therefore, we get the value of $k = 12$ which is the radius of gyration of the object through the center of mass.

Note: A Radius of Gyration in general is the distance from the center of mass of a body at which the whole mass could be concentrated without changing its moment of rotational inertia about an axis through the center of mass.