Question

If the product of perpendiculars from the foci upon the polar of P be constant and equal to ${{c}^{2}}$, prove that the locus of P is the ellipse ${{b}^{4}}{{x}^{2}}\left( {{c}^{2}}+{{a}^{2}}{{c}^{2}} \right)+{{c}^{2}}{{a}^{4}}{{y}^{2}}={{a}^{4}}{{b}^{4}}$.

Answer 1

Write the equation of polar with respect to pole and calculate perpendicular distance from foci. Then use the given condition for the question.

Complete answer:
Let us suppose the ellipse given is,
$\dfrac{{{x}^{2}}}{a{}^{2}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1............(i)(a>b)$(For proving purpose)
Note that it may be $\left( b < a \right)$ as well.

As we know that polar is the line with respect to pole in ellipse in a way like: -
As there are infinite numbers of lines can be drawn through P and each can be termed as chord and cut at two points at two points to ellipse. Tangents (two) can be drawn through each chord and ellipse intersection point as shown below: -
$\dfrac{{{x}^{2}}}{a{}^{2}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$

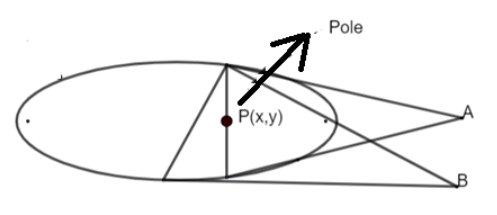
Line joining the points A and B will be termed as polar i.e. all the points we get after drawing two tangents with respect to P (pole) will lie on a line which is called polar and the equation of that line is $T=0$ .
That is,
$\dfrac{x{{x}_{1}}}{{{a}^{2}}}+\dfrac{y{{y}_{1}}}{b{}^{2}}=1$
Now, coming to question, the equation of ellipse is,
$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{b{}^{2}}=1$
Pole assumed is $P\text{ }\left( h,\text{ }k \right)$.
Now the polar with respect to pole that is$T=0$, is
$\dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}}=1.........(ii)$
Foci of ellipse are $(ae,0),(-ae,0)$.
Perpendicular distance from foci are
${{P}_{1}}=\dfrac{\dfrac{h(ae)}{{{a}^{2}}}+0-1}{\sqrt{{{\left( \dfrac{h}{{{a}^{2}}} \right)}^{2}}+{{\left( \dfrac{k}{{{b}^{2}}} \right)}^{2}}}}$
($\because$Perpendicular distance of a point $\left( {{x}_{1}},{{y}_{1}} \right)$from $ax+by+c=0$is $\left| \dfrac{a{{x}_{1}}+b{{y}_{1}}+c}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right|$)
${{P}_{1}}=\dfrac{\dfrac{hae}{{{a}^{2}}}-1}{\sqrt{\dfrac{{{h}^{2}}}{{{a}^{4}}}+\dfrac{{{k}^{2}}}{{{b}^{4}}}}}..........(iii)$
Similarly,
${{P}_{2}}=\dfrac{\dfrac{h(-ae)}{{{a}^{2}}}+0-1}{\sqrt{\dfrac{{{h}^{2}}}{{{a}^{4}}}+\dfrac{{{k}^{2}}}{{{b}^{4}}}}}...........(iv)$($\because$Distance from $-ae,0$)
As we have given that product of ${{P}_{1}}\And {{P}_{2}}$is constant and equal to ${{c}^{2}}$. Therefore,
${{P}_{1}}{{P}_{2}}={{c}^{2}}$
Substituting values from equation (iii) and (iv), we get
$\dfrac{\left( \dfrac{hae}{{{a}^{2}}}-1 \right)\left( \dfrac{-hae}{{{a}^{2}}}-1 \right)}{\dfrac{{{h}^{2}}}{{{a}^{4}}}+\dfrac{{{k}^{2}}}{{{b}^{4}}}}={{c}^{2}}$
Cancelling the like terms, we get
$\dfrac{\left( \dfrac{he}{a}-1 \right)\left( \dfrac{he}{a}+1 \right)}{\dfrac{{{h}^{2}}}{{{a}^{4}}}+\dfrac{{{k}^{2}}}{{{b}^{4}}}}=-{{c}^{2}}$
For getting locus we need to replace $\left( h,\text{ }k \right)$ to $\left( x,\text{ }y \right)$ for generalized/ standard form and also cross multiplying, we get
$\left( \dfrac{xe}{a}-1 \right)\left( \dfrac{xe}{a}+1 \right)=-{{c}^{2}}\left( \dfrac{{{x}^{2}}}{{{a}^{4}}}+\dfrac{{{y}^{2}}}{{{b}^{4}}} \right)$
We know $({{a}^{2}}-{{b}^{2}})=(a+b)(a-b)$ , so the above equation can be written as,
$\dfrac{{{x}^{2}}{{e}^{2}}}{{{a}^{2}}}-1=-{{c}^{2}}\left( \dfrac{{{x}^{2}}{{b}^{4}}+{{y}^{2}}{{a}^{4}}}{{{a}^{4}}{{b}^{4}}} \right)$
On cross multiplication, we get
${{x}^{2}}{{e}^{2}}{{a}^{2}}{{b}^{4}}-{{a}^{4}}{{b}^{4}}=-{{x}^{2}}{{c}^{2}}{{b}^{4}}-{{y}^{2}}{{a}^{4}}{{c}^{2}}$
Taking out the common terms, we get
${{x}^{2}}{{b}^{4}}\left( {{c}^{2}}+{{a}^{2}}{{e}^{2}} \right)+{{c}^{2}}{{a}^{4}}{{y}^{2}}={{a}^{4}}{{b}^{4}}$
Hence proved,

Note:
Students need to clear about the concepts of pole and polar equations as well. Calculation is a more important portion as well. For proving any question like this we need to assume standard equations and points wherever necessary to keep the flexibility of the solution.