Question

If the points of intersection of the line $4x-3y-10=0$ and the circle ${{x}^{2}}+{{y}^{2}}-2x+4y-20=0$ are $(a,b)$ and $(c,d)$ where $a$ and $b$ are positive and $c$ and $d$ are negative, then $a-c+b+d$ is ____.

Answer 1

Hint: Rewrite the equation of the line in terms of one of the variables and then substitute it in the equation of the circle. Solve the equation to get their points of intersection and thus, the value of $a-c+b+d$.

Complete step by step answer:
We have the equation of a line $4x-3y-10=0$ and a circle ${{x}^{2}}+{{y}^{2}}-2x+4y-20=0$. We have to find the points of intersection of the two curves.
We will find their point of intersection by substituting the equation of one curve into the equation of another curve and then solving them to find their point of intersection.

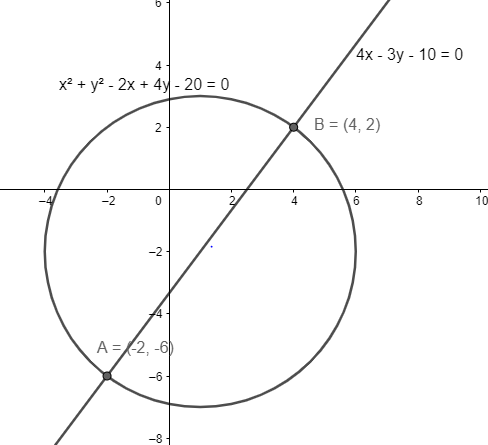
We can rewrite the equation of line by writing $x$ in terms of $y$. Rearranging the terms of the equation of line $4x-3y-10=0$, we get $x=\dfrac{3y+10}{4}$.
We will substitute this equation of line in the equation of circle ${{x}^{2}}+{{y}^{2}}-2x+4y-20=0$.
Thus, we have ${{\left( \dfrac{3y+10}{4} \right)}^{2}}+{{y}^{2}}-2\left( \dfrac{3y+10}{4} \right)+4y-20=0$ as the equation of circle.
Solving the above equation, we get $\dfrac{9{{y}^{2}}+100+60y}{16}+{{y}^{2}}-\left( \dfrac{3y+10}{2} \right)+4y-20=0$.
We will further simplify the equation by taking LCM.
Thus, we have $9{{y}^{2}}+100+60y+16{{y}^{2}}-24y-80+64y-320=0$
$\Rightarrow 25{{y}^{2}}+100y-300=0$
Dividing the equation by $25$, we get ${{y}^{2}}+4y-12=0$.
Factorizing the above equation, we have ${{y}^{2}}+6y-2y-12=0$

& \Rightarrow y\left( y+6 \right)-2\left( y+6 \right)=0 \\\ & \Rightarrow \left( y+6 \right)\left( y-2 \right)=0 \\\ & \Rightarrow y=2,-6 \\\ \end{aligned}$$ Substituting the values $$y=2,-6$$ in the equation of line $$x=\dfrac{3y+10}{4}$$, we get $$x=4,-2$$. Thus, the two points of intersection of the two curves are $$\left( 4,2 \right),\left( -2,-6 \right)$$. We know that $$a$$ and $$b$$ are positive and $$c$$ and $$d$$ are negative. Thus, we have $$a=4,b=2,c=-2,d=-6$$. Now, we have to find the value of $$a-c+b+d$$ . Substituting the values, we get $$a-c+b+d=4+2+2-6=2$$. _Hence, the value of $$a-c+b+d$$ is $$2$$._ Note: We can also solve this question by rearranging the equation of line by writing $$y$$ in terms of $$x$$ and then substituting it in the equation of circle and solving it to get the required points of intersection.