Question

If the points A(2, 1, -1), B(0, -1, 0), C(4, 0, 4) and D(2, 0, x) are coplanar then x =

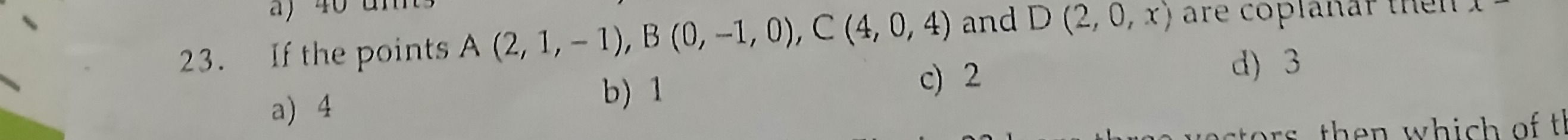
• A. 4
• B. 1
• C. 2
• D. 3

Answer 1

Answer: (B)

1

Answer 2

To determine the value of x for which the points A(2, 1, -1), B(0, -1, 0), C(4, 0, 4), and D(2, 0, x) are coplanar, we can use the scalar triple product.

1. Form Vectors: We first find the vectors $\vec{AB}$, $\vec{AC}$, and $\vec{AD}$.

   $$\begin{aligned} \vec{AB} &= B - A = (0-2, -1-1, 0-(-1)) = (-2, -2, 1) \\ \vec{AC} &= C - A = (4-2, 0-1, 4-(-1)) = (2, -1, 5) \\ \vec{AD} &= D - A = (2-2, 0-1, x-(-1)) = (0, -1, x+1) \end{aligned}$$

2. Scalar Triple Product: For the points to be coplanar, the scalar triple product $\vec{AB} \cdot (\vec{AC} \times \vec{AD})$ must be zero.

3. Compute Cross Product: Compute the cross product $\vec{AC} \times \vec{AD}$.

   $$\vec{AC} \times \vec{AD} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 2 & -1 & 5 \\ 0 & -1 & x+1 \\ \end{vmatrix} = \mathbf{i}[(-1)(x+1)-5(-1)] - \mathbf{j}[2(x+1)-5(0)] + \mathbf{k}[2(-1)-(-1)(0)]$$ $$= \mathbf{i}[-(x+1)+5] - \mathbf{j}[2x+2] + \mathbf{k}[-2] = \mathbf{i}(4-x) - \mathbf{j}(2x+2) - 2\mathbf{k}$$

4. Compute Scalar Triple Product: Compute the scalar triple product $\vec{AB} \cdot (\vec{AC} \times \vec{AD})$.

   $$\vec{AB} \cdot (\vec{AC} \times \vec{AD}) = (-2)(4-x) + (-2)[-(2x+2)] + (1)(-2)$$ $$= -8 + 2x + 4x + 4 - 2 = 6x - 6$$

5. Solve for x: Set the scalar triple product equal to zero and solve for $x$.

   $$6x - 6 = 0 \implies 6x = 6 \implies x = 1$$

Thus, the value of $x$ is 1.