Question

If the points $A(a, 0)$, $B(0, b)$ and $C(1, 1)$ are collinear then-
$\begin{aligned} &{\text{A}}.\;\dfrac{1}{{\text{a}}} + \dfrac{1}{{\text{b}}} = 1 \\\ &{\text{B}}.\;{\text{a}} + {\text{b}} = 1 \\\ &{\text{C}}.\;{\text{a}} + {\text{b}} = 2 \\\ &{\text{D}}.\;\dfrac{1}{{\text{a}}} - \dfrac{1}{{\text{b}}} = 1 \\\ \end{aligned}$

Answer 1

Hint: For the points to be collinear, the area of the triangle formed by these three points as vertices should be equal to zero. We will use this formula to find the relation between a and b. Mathematically it is given as-
$\dfrac{1}{2}\left[ {{{\text{x}}_1}\left( {{{\text{y}}_2} - {{\text{y}}_3}} \right) + {{\text{x}}_2}\left( {{{\text{y}}_3} - {{\text{y}}_1}} \right) + {{\text{x}}_3}\left( {{{\text{y}}_1} - {{\text{y}}_2}} \right)} \right] = 0$

Complete step-by-step answer:
We have been given that the points $A(a, 0)$, $B(0, b)$ and $C(1, 1)$ are collinear. This means that the area of the triangle formed by these three points is zero.

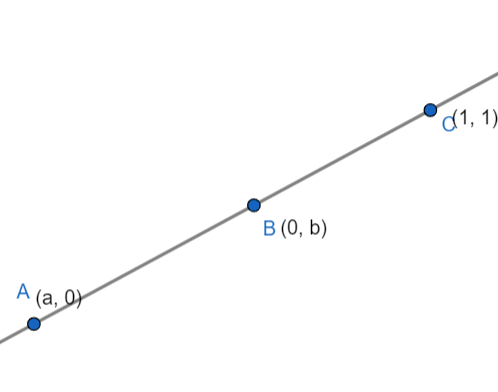
Let $A(a, 0)$, $B(0, b)$ and $C(1, 1)$. We will apply the triangle formula to these three points as-
$\begin{aligned} &\dfrac{1}{2}\left[ {{\text{a}}\left( {{\text{b}} - 1} \right) + 0\left( {1 - 0} \right) + 1\left( {0 - {\text{b}}} \right)} \right] = 0 \\\ &ab; \- {\text{a}} - {\text{b}} = 0 \\\ &{\text{a}} + {\text{b}} = ab \\\ \end{aligned}$
Dividing this by ab,
$\dfrac{1}{{\text{b}}} + \dfrac{1}{{\text{a}}} = 1 \\\$

By this equation we can see that the correct option is A.

Note: In such types of questions, we need to use a particular property of collinear points to form the equation. Another condition for the points to be collinear is that the slope of any two pairs are equal. That is-
$\begin{aligned} &Slop;{e_{AB}} = Slop{e_{BC}} \\\ &\dfrac{{{\text{b}} - 0}}{{0 - {\text{a}}}} = \dfrac{{{\text{b}} - 1}}{{0 - 1}} \\\ &\dfrac{{\text{b}}}{{\text{a}}} = - \left( {{\text{b}} - 1} \right) \\\ &{\text{b}} = ab - {\text{a}} \\\ &{\text{a}} + {\text{b}} = ab \\\ &\dfrac{1}{{\text{a}}} + \dfrac{1}{{\text{b}}} = 1 \\\ \end{aligned}$