Question

If the points A (1, -2), B (2, 3) and C (a, 2) and D (-4, -3) form a parallelogram. Find the value of ‘a’ and height of the parallelogram taking AB as base.

Answer 1

Hint – Use the property that the diagonals of the parallelogram bisect each other , so from this if we compare the midpoints of both diagonals we will get $a$, Now for height compare the area the area of the parallelogram in two different forms, that is one using determinant formula for area of triangle and another using height and base multiplication of a triangle formula.

Complete step-by-step answer:

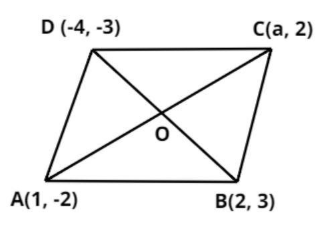
Let us consider the parallelogram ABCD as shown above.
As we know that the midpoints of the diagonal are equal.
Therefore midpoint of AC = midpoint of BD
A = ($x_1$, $y_1$) = (1, -2)
B = ($x_2$, $y_2$) = (2, 3)
C = ($x_3$, $y_3$) = (a, 2)
D = ($x_4$, $y_4$) = (-4, -3)
Now apply midpoint formula we have,
$\Rightarrow \left( {\dfrac{{{x_1} + {x_3}}}{2},\dfrac{{{y_1} + {y_3}}}{2}} \right) = \left( {\dfrac{{{x_2} + {x_4}}}{2},\dfrac{{{y_2} + {y_4}}}{2}} \right)$
$\Rightarrow \left( {\dfrac{{1 + a}}{2},\dfrac{{ - 2 + 2}}{2}} \right) = \left( {\dfrac{{2 - 4}}{2},\dfrac{{3 - 3}}{2}} \right)$
$\Rightarrow \left( {\dfrac{{a + 1}}{2},0} \right) = \left( { - 1,0} \right)$
So on comparing we have,
$\Rightarrow \dfrac{{a + 1}}{2} = - 1$
$\Rightarrow a + 1 = - 2$
$\Rightarrow a = - 3$
Now as we know that the area of the parallelogram (ABCD) = $2 \times$area of triangle ABD.
So first calculate area of triangle ABD
So area of triangle ABD = \dfrac{1}{2}\left| {\begin{array}{*{20}{c}} {{x_1}}&{{y_1}}&1 \\\ {{x_2}}&{{y_2}}&1 \\\ {{x_3}}&{{y_3}}&1 \end{array}} \right|
Let A = ($x_1$, $y_1$) = (1, -2)
B = ($x_2$, $y_2$) = (2, 3)
D = ($x_3$, $y_3$) = (-4, -3)
Therefore area (A) of triangle ABD = \dfrac{1}{2}\left| {\begin{array}{*{20}{c}} 1&{ - 2}&1 \\\ 2&3&1 \\\ { - 4}&{ - 3}&1 \end{array}} \right|
Now expand the determinant we have,
A = \dfrac{1}{2}\left[ {1\left| {\begin{array}{*{20}{c}} 3&1 \\\ { - 3}&1 \end{array}} \right| - \left( { - 2} \right)\left| {\begin{array}{*{20}{c}} 2&1 \\\ { - 4}&1 \end{array}} \right| + 1\left| {\begin{array}{*{20}{c}} 2&3 \\\ { - 4}&{ - 3} \end{array}} \right|} \right]
Now simplify it we have,
A = $\dfrac{1}{2}\left[ {1\left( {3 + 3} \right) + 2\left( {2 + 4} \right) + 1\left( { - 6 + 12} \right)} \right]$
A = $\dfrac{1}{2}\left[ {6 + 12 + 6} \right] = \dfrac{{24}}{2} = 12$ sq. units.
So the area of parallelogram = $2 \times 12 = 24$ sq. units.
Now as we know that the area of the triangle is half multiplied by base (b) and height (h).
So area of parallelogram = $2 \times \dfrac{1}{2} \times h \times b$
$\Rightarrow h = \dfrac{{24}}{b}$ unit.
Now it is given that AB is the base.
So the distance of AB is calculated as
$\Rightarrow AB = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
A = ($x_1$, $y_1$) = (1, -2)
B = ($x_2$, $y_2$) = (2, 3)
So the distance AB is
$\Rightarrow AB = b = \sqrt {{{\left( {2 - 1} \right)}^2} + {{\left( {3 - \left( { - 2} \right)} \right)}^2}} = \sqrt {{1^2} + {5^2}} = \sqrt {26}$ unit.
So the height of the parallelogram is
$\Rightarrow h = \dfrac{{24}}{{\sqrt {26} }}$ unit.
So this is the required height of the parallelogram.

Note – A parallelogram is a quadrilateral with opposite sides parallel and therefore opposite angles are equal. A quadrilateral with equal sides is called a rhombus and a parallelogram with all angles as right angles is called a rectangle. Also a diagonal of a parallelogram divides its area in two equal parts which is what we have used in calculating the height of the parallelogram.