Question

If the points $(-1,-1,2),(2,m,5)\,and\,(3,11,6)$ are collinear, then find the value of m.
(A). 6
(B). 8
(C). 10
(D). 12

Answer 1

Hint: Assume three points P, Q, and R whose coordinates are $(-1,-1,2),(2,m,5)\,and\,(3,11,6)$ respectively. Express the coordinates of the points P, Q, and R in the vector form as $\overrightarrow{P}=-1\overset{\hat{\ }}{\mathop{i}}\,-1\overset{\hat{\ }}{\mathop{j}}\,+2\overset{\hat{\ }}{\mathop{k}}\,$ , $\overrightarrow{Q}=2\overset{\hat{\ }}{\mathop{i}}\,+m\overset{\hat{\ }}{\mathop{j}}\,+5\overset{\hat{\ }}{\mathop{k}}\,$ , and $\overrightarrow{R}=3\overset{\hat{\ }}{\mathop{i}}\,+11\overset{\hat{\ }}{\mathop{j}}\,+6\overset{\hat{\ }}{\mathop{k}}\,$ . If the points P, Q, and R is collinear then,$\overrightarrow{PQ}=\lambda \overrightarrow{QR}$ where $\overrightarrow{PQ}=\overrightarrow{P}-\overrightarrow{Q}$ and $\overrightarrow{QR}=\overrightarrow{Q}-\overrightarrow{R}$ . Now compare LHS and RHS and solve it further.

Complete step-by-step solution -
Assume three points P, Q, and R whose coordinates are $(-1,-1,2),(2,m,5)\,and\,(3,11,6)$ respectively.
If three points are collinear then all the three points lie on the same line.

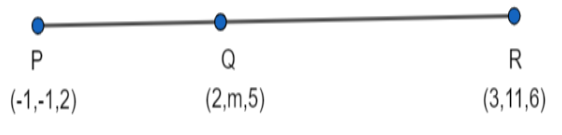
Express the coordinates of the points P, Q, and R in the vector form.
Converting the coordinates of the points P, Q, and R in the vector form, we get
$\overrightarrow{P}=-1\overset{\hat{\ }}{\mathop{i}}\,-1\overset{\hat{\ }}{\mathop{j}}\,+2\overset{\hat{\ }}{\mathop{k}}\,$ ……………….(1)
$\overrightarrow{Q}=2\overset{\hat{\ }}{\mathop{i}}\,+m\overset{\hat{\ }}{\mathop{j}}\,+5\overset{\hat{\ }}{\mathop{k}}\,$ ……………….(2)
$\overrightarrow{R}=3\overset{\hat{\ }}{\mathop{i}}\,+11\overset{\hat{\ }}{\mathop{j}}\,+6\overset{\hat{\ }}{\mathop{k}}\,$ ……………….(3)
If the points P, Q, and R is collinear then,
$\overrightarrow{PQ}=\lambda \overrightarrow{QR}$ …………….(4)
Now, the value of the $\overrightarrow{PQ}$ is,
$\overrightarrow{PQ}=\overrightarrow{P}-\overrightarrow{Q}$ ……………..(5)
Putting the value of $\overrightarrow{P}$ and $\overrightarrow{Q}$ from equation (1) and equation (2) in equation (5), we get
$\overrightarrow{PQ}=(-1\overset{\hat{\ }}{\mathop{i}}\,-1\overset{\hat{\ }}{\mathop{j}}\,+2\overset{\hat{\ }}{\mathop{k}}\,)-(2\overset{\hat{\ }}{\mathop{i}}\,+m\overset{\hat{\ }}{\mathop{j}}\,+5\overset{\hat{\ }}{\mathop{k}}\,)$
$\Rightarrow \overrightarrow{PQ}=-3\overset{\hat{\ }}{\mathop{i}}\,-(m+1)\overset{\hat{\ }}{\mathop{j}}\,-3\overset{\hat{\ }}{\mathop{k}}\,$ ……………………(6)
Now, the value of the $\overrightarrow{QR}$ is,
$\overrightarrow{QR}=\overrightarrow{Q}-\overrightarrow{R}$ ……………..(7)
Putting the value of $\overrightarrow{Q}$ and $\overrightarrow{R}$ from equation (2) and equation (3) in equation (7), we get
$\overrightarrow{QR}=2\overset{\hat{\ }}{\mathop{i}}\,+m\overset{\hat{\ }}{\mathop{j}}\,+5\overset{\hat{\ }}{\mathop{k}}\,-3\overset{\hat{\ }}{\mathop{i}}\,-11\overset{\hat{\ }}{\mathop{j}}\,-6\overset{\hat{\ }}{\mathop{k}}\,$
$\Rightarrow \overrightarrow{QR}=-1\overset{\hat{\ }}{\mathop{i}}\,+(m-11)\overset{\hat{\ }}{\mathop{j}}\,-1\overset{\hat{\ }}{\mathop{k}}\,$ ………………………(8)
From equation (4), we have $\overrightarrow{PQ}=\lambda \overrightarrow{QR}$ .
Now, putting the value of $\overrightarrow{PQ}$ and $\overrightarrow{QR}$ from equation (6) and equation (8) in equation (4), we get
$\overrightarrow{PQ}=\lambda \overrightarrow{QR}$
$\Rightarrow -3\overset{\hat{\ }}{\mathop{i}}\,-(m+1)\overset{\hat{\ }}{\mathop{j}}\,-3\overset{\hat{\ }}{\mathop{k}}\,=\lambda \\{-1\overset{\hat{\ }}{\mathop{i}}\,+(m-11)\overset{\hat{\ }}{\mathop{j}}\,-1\overset{\hat{\ }}{\mathop{k}}\,\\}$
On comparing LHS and RHS of the above equation, we get
$-3=-\lambda$ ……………………..(9)
$-(m+1)=\lambda (m-11)$ ………………….(10)
Solving equation (1), we get
$-3=-\lambda$
$\Rightarrow 3=\lambda$ …………………(11)
Now, putting the value of $\lambda$ in equation (10), we get
$-(m+1)=\lambda (m-11)$

& -(m+1)=3(m-11) \\\ & \Rightarrow -m-1=3m-33 \\\ & \Rightarrow 33-1=3m+m \\\ & \Rightarrow 32=4m \\\ & \Rightarrow 8=m \\\ \end{aligned}$$ So, the value of m is 8. Hence, the correct option is (B). Note: We can also solve this question using another method. If the points $$\overrightarrow{P}=-1\overset{\hat{\ }}{\mathop{i}}\,-1\overset{\hat{\ }}{\mathop{j}}\,+2\overset{\hat{\ }}{\mathop{k}}\,$$ , $$\overrightarrow{Q}=2\overset{\hat{\ }}{\mathop{i}}\,+m\overset{\hat{\ }}{\mathop{j}}\,+5\overset{\hat{\ }}{\mathop{k}}\,$$ and $$\overrightarrow{R}=3\overset{\hat{\ }}{\mathop{i}}\,+11\overset{\hat{\ }}{\mathop{j}}\,+6\overset{\hat{\ }}{\mathop{k}}\,$$ are collinear then $$\overrightarrow{PQ}=-3\overset{\hat{\ }}{\mathop{i}}\,-(m+1)\overset{\hat{\ }}{\mathop{j}}\,-3\overset{\hat{\ }}{\mathop{k}}\,$$ must be parallel to $$\overrightarrow{QR}=-1\overset{\hat{\ }}{\mathop{i}}\,+(m-11)\overset{\hat{\ }}{\mathop{j}}\,-1\overset{\hat{\ }}{\mathop{k}}\,$$ . Hence, the ratios of corresponding direction ratios of parallel $$\overrightarrow{PQ}=-3\overset{\hat{\ }}{\mathop{i}}\,-(m+1)\overset{\hat{\ }}{\mathop{j}}\,-3\overset{\hat{\ }}{\mathop{k}}\,$$ and $$\overrightarrow{QR}=-1\overset{\hat{\ }}{\mathop{i}}\,+(m-11)\overset{\hat{\ }}{\mathop{j}}\,-1\overset{\hat{\ }}{\mathop{k}}\,$$ must be equal. So, $$\dfrac{-3}{-1}=\dfrac{-(m+1)}{(m-11)}=\dfrac{-3}{-1}$$ . Now, $$\begin{aligned} & \dfrac{-3}{-1}=\dfrac{-(m+1)}{(m-11)} \\\ & \Rightarrow -3\left( m-11 \right)=\left( m+1 \right) \\\ & \Rightarrow -3m+33=m+1 \\\ & \Rightarrow 33-1=3m+m \\\ & \Rightarrow 32=4m \\\ & \Rightarrow 8=m \\\ \end{aligned}$$ So, the value of m is 8. Hence, the correct option is (B).