Question

If the points (1, 1), (2, 3) and (5, -1) form a right triangle, then the hypotenuse is of length
(a) 3
(b) 4
(c) 6
(d) 5

Answer 1

Hint : To solve this question we will first of all assume some variables A, B and C for the given set of points and then determine which of triangle ABC is larger in length. That side would be the hypotenuse. This can be done using distance formula which is,
$D=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$, where A = $\left( {{x}_{1}},{{y}_{1}} \right)$ & B = $\left( {{x}_{2}},{{y}_{2}} \right)$.

Complete step-by-step answer :
We will use a distance formula to solve this question.
Let A = (1, 1), B = (2, 3) and C = (5, -1).
Distance formula to determine distance between two points P (x, y) and Q (z, t) is,
$D=PQ=\sqrt{{{\left( x-z \right)}^{2}}+{{\left( y-t \right)}^{2}}}$
Using distance formula the distance between A and B is,
$AB=\sqrt{{{\left( 1-2 \right)}^{2}}+{{\left( 1-3 \right)}^{2}}}$
Squaring both sides we get,
$\Rightarrow {{\left( AB \right)}^{2}}={{1}^{2}}+{{\left( 2 \right)}^{2}}$
$\Rightarrow {{\left( AB \right)}^{2}}=5$ - (1)
Similarly, $BC=\sqrt{{{\left( 2-5 \right)}^{2}}+{{\left( 3+1 \right)}^{2}}}$.
Squaring both sides,
$\Rightarrow {{\left( BC \right)}^{2}}=\left( 9+16 \right)$
$\Rightarrow {{\left( BC \right)}^{2}}=25$ - (2)
Again, $AC=\sqrt{{{\left( 1-5 \right)}^{2}}+{{\left( 1+1 \right)}^{2}}}$
Squaring both sides,
$\Rightarrow {{\left( AC \right)}^{2}}=16+4$
$\Rightarrow {{\left( AC \right)}^{2}}=20$ - (3)
From (1), (2) and (3) we get that the side BC is largest of all.
Hence BC is hypotenuse.
It’s length is, ${{\left( BC \right)}^{2}}=25$.
$\Rightarrow BC=5$.

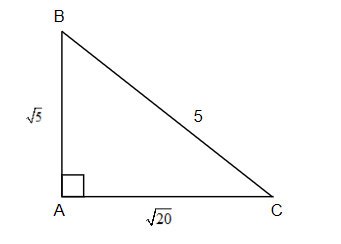
So, the correct answer is “Option D”.

Note : Students may be confused at the point where the square of the BC side is taken rather than BC itself. This is correct as hypotenuse is the biggest side then its square is also the biggest square of all other sides. Students can also find the sides by taking the square root on both sides as,
AB = $\sqrt{5}=2.23$
AC = $\sqrt{20}=4.47$
BC = $\sqrt{25}=5$
So, from the above, it is clear that BC is the longest side.