Question

If the points (0,4), (4,0) and (6,2p) are collinear, then the value of p is
(a) -1
(b) 7
(c) 6
(d) 4

Answer 1

To solve this question, firstly we will find the slope of line joining the points A and B, then we will find the slope of line joining the points B and C. After that, using the concept of collinearity of three or more points, we will put the slopes of lines equal to each other, then we will find the value of p.

Complete step-by-step answer:
In question, it is given that the points (0,4), (4,0) and (6,2p) are collinear.
Let us see first what is the meaning and condition of the collinear of points.
When the number of points lying in the same straight line, then the points are called collinear points, or we can say that three or more points are collinear, if the slopes of any two pairs of points is the same.
Now, as the points (0,4), (4,0) and (6,2p) are collinear, so we can say that line joining points (0,4) and (4,0) and line joining points (4,0) and (6,2p) will have the same slopes.
So, let points be A(0,4), B(4,0) and C(6,2p) and line joining point A and B will be AB and line joining point B and C will be BC.

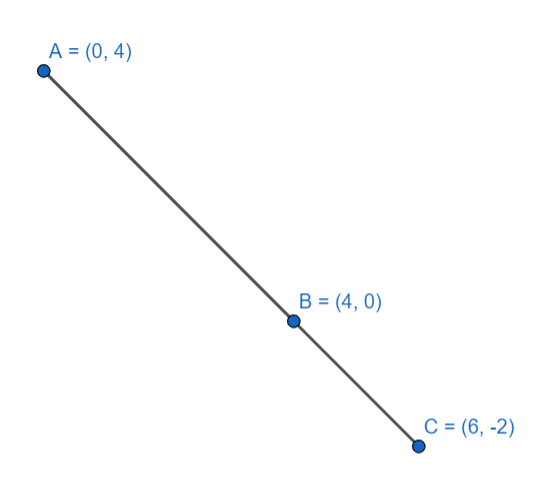
Now, we know the concept that if A(a,b) and B(c,d), then slope of line AB is equals to $\dfrac{d-b}{c-a}$ .
So, slope of line joining point A and B will be $\dfrac{0-4}{4-0}$
On simplifying, we get
Slope of AB = -1
And, slope of line joining point B and C will be $\dfrac{2p-0}{6-4}$
On simplifying, we get
Slope of BC = p
As, points A, B and C are collinear, so
Slope of AB = Slope of BC
Then, p = -1

So, the correct answer is “Option A”.

Note: Always remember that when three or more points are collinear, then the slopes of any two pairs of points are the same. Keep in mind that, if $A({{x}_{1}},{{y}_{1}})$ and $B({{x}_{2}},{{y}_{2}})$, then slope of line AB is equals to $\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ . Also, while evaluating the slope of lines, try not to make any calculation errors.