Solveeit Logo
Login

Question

Question: If the point \[\hat{i}+\hat{j}\] , \[\hat{i}-\hat{j}\] and \(p\hat{i}+q\hat{j}+r\hat{k}\) are collin...

If the point i^+j^\hat{i}+\hat{j} , i^−j^\hat{i}-\hat{j} and pi^+qj^+rk^p\hat{i}+q\hat{j}+r\hat{k} are collinear, then
a)p=1 b)r=0 c)q∈R d)q≠1 \begin{aligned} & a)p=1 \\\ & b)r=0 \\\ & c)q\in R \\\ & d)q\ne 1 \\\ \end{aligned}

Explanation

Solution

Now we know that the given points are collinear. Let us say A = i^+j^\hat{i}+\hat{j} , C = i^−j^\hat{i}-\hat{j} and B = pi^+qj^+rk^p\hat{i}+q\hat{j}+r\hat{k}. Now we know that the angle between AC and BC is 0. Hence we will take the cross product of AB and BC. Hence we will find the required condition.

Complete step by step answer:
Now let us consider the three point A = i^+j^\hat{i}+\hat{j} , C = i^−j^\hat{i}-\hat{j} and B = pi^+qj^+rk^p\hat{i}+q\hat{j}+r\hat{k} . We know that the points are collinear.

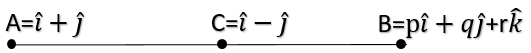
Now we know first let us calculate CA.
CA = i^−j^−(i^+j^)=−2j^\hat{i}-\hat{j}-\left( \hat{i}+\hat{j} \right)=-2\hat{j}
Now let us calculate BC.
BC=pi^+qj^+rk^−(i^−j^)=(p−1)i^+(q+1)j^+rk^BC=p\hat{i}+q\hat{j}+r\hat{k}-\left( \hat{i}-\hat{j} \right)=\left( p-1 \right)\hat{i}+\left( q+1 \right)\hat{j}+r\hat{k}
Now we know that ABC are collinear hence the angle between AC and BC is 0.
Now we know that AC×BC=∣AB∣∣BC∣sin⁡θAC\times BC=|AB||BC|\sin \theta
Here we have the angle is 0. Hence we get sin⁡θ=0\sin \theta =0
Now we have AC×BC=0AC\times BC=0
Hence we have (−2j^)×[(p−1)i^+(q+1)j^+rk^]=0\left( -2\hat{j} \right)\times \left[ \left( p-1 \right)\hat{i}+\left( q+1 \right)\hat{j}+r\hat{k} \right]=0
Now we know that j^×i^=−k^\hat{j}\times \hat{i}=-\hat{k}, j^×j^=0\hat{j}\times \hat{j}=0 and j^×k^=i^\hat{j}\times \hat{k}=\hat{i}
Hence we get,
[−(−2p+2)k^+(0)+(−2r)i^]=0\left[ -\left( -2p+2 \right)\hat{k}+\left( 0 \right)+\left( -2r \right)\hat{i} \right]=0
Hence we have 2r=02r=0 and −2p+2=0-2p+2=0
Now consider 2r = 0.
Dividing the equation by 2 we get, r = 0.
Now consider the equation -2p + 2 = 0
Now rearranging the terms we get, 2p = 2
Dividing the whole equation by 2 we get p = 1.
Hence we get, p = 1 and r = 0.
Now there is no condition on q hence we can say that q∈Rq\in R

So, the correct answer is “Option A, B and C”.

Note: Now note that for any two vectors we have if the vectors are perpendicular their dot product is 0 and if they are parallel the cross product is 0. Also in general we can calculate cross product of two vectors ai^+bj^+ck^a\hat{i}+b\hat{j}+c\hat{k} and pi^+qj^+rk^p\hat{i}+q\hat{j}+r\hat{k} is given by ∣i^j^k^ abc pqr ∣=0\left| \begin{matrix} {\hat{i}} & {\hat{j}} & {\hat{k}} \\\ a & b & c \\\ p & q & r \\\ \end{matrix} \right|=0 .