Question

If the perpendicular is let fall from the point P on parabola upon its polar. Prove that the distance of the foot of this perpendicular from the focus is equal to the distance of point P from its directrix.

Answer 1

The rough figure drawn based on the given information is

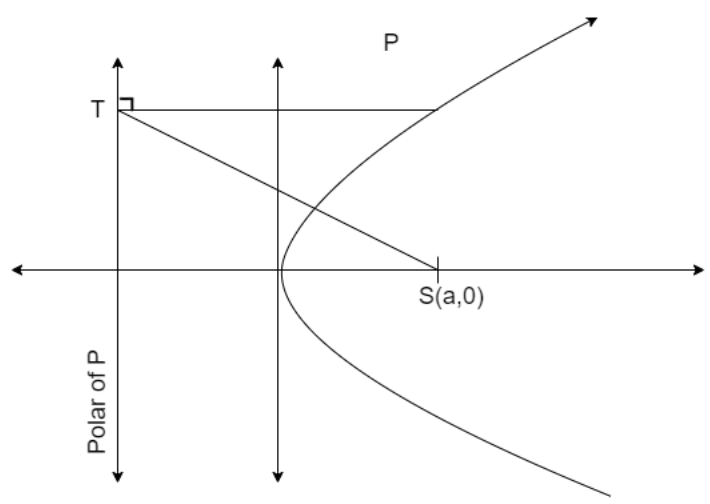
We assume that equation of parabola as ${{y}^{2}}=4ax$ then equation of directrix is given as
$x+a=0$ then we assume that point P as $\left( h,k \right)$ to find the polar of point P with respect to parabola $S\equiv {{y}^{2}}=4ax$ given as ${{S}_{1}}=0$ where
${{S}_{1}}=yk-2a\left( x+h \right)$
Then we find the foot of perpendicular of point $P\left( h,k \right)$ to its polar $ax+by+c=0$ given as
$\dfrac{x-h}{a}=\dfrac{y-k}{b}=\dfrac{-\left( ah+bk+c \right)}{{{a}^{2}}+{{b}^{2}}}$
Then we find the distance between focus ‘S’ and foot of perpendicular ‘T’ using distance formula that is the formula of distance between $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ is given as
$ST=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$
Then we find the distance of point P to the directrix using perpendicular formula that is the distance of $P\left( h,k \right)$ to line $ax+by+c=0$ is given as
$D=\dfrac{\left| ah+bk+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$

Complete step-by-step solution:
Let us assume that the equation of parabola as
$\Rightarrow {{y}^{2}}=4ax$
Let us assume the point P as $P\left( h,k \right)$
We know that the equation of polar of point P with respect to parabola $S\equiv {{y}^{2}}=4ax$ given as ${{S}_{1}}=0$ where
${{S}_{1}}=yk-2a\left( x+h \right)$
By using the above formula we get the equation of polar of P as

& \Rightarrow yk-2a\left( x+h \right)=0 \\\ & \Rightarrow 2ax-ky+2ah=0 \\\ \end{aligned}$$ Now, let us find the foot of perpendicular of $$P\left( h,k \right)$$ on its polar which is $$'T'$$ We know that we can find the foot of perpendicular of point $$P\left( h,k \right)$$ to its polar $$ax+by+c=0$$ given as $$\dfrac{x-h}{a}=\dfrac{y-k}{b}=\dfrac{-\left( ah+bk+c \right)}{{{a}^{2}}+{{b}^{2}}}$$ By using the above formula we get the co – ordinates of point $$'T'$$ as $$\begin{aligned} & \Rightarrow \dfrac{x-h}{2a}=\dfrac{y-k}{-k}=\dfrac{-\left( 2ah-{{k}^{2}}+2ah \right)}{4{{a}^{2}}+{{k}^{2}}} \\\ & \Rightarrow \dfrac{x-h}{2a}=\dfrac{y-k}{-k}=\dfrac{{{k}^{2}}-4ah}{4{{a}^{2}}+{{k}^{2}}} \\\ \end{aligned}$$ By dividing the terms we get the $$'x'$$ co – ordinate of $$'T'$$ as $$\begin{aligned} & \Rightarrow \dfrac{x-h}{2a}=\dfrac{{{k}^{2}}-4ah}{4{{a}^{2}}+{{k}^{2}}} \\\ & \Rightarrow x=h+\dfrac{2a{{k}^{2}}-8{{a}^{2}}h}{4{{a}^{2}}+{{k}^{2}}} \\\ \end{aligned}$$ By doing the LCM and adding the terms we get $$\begin{aligned} & \Rightarrow x=\dfrac{4{{a}^{2}}h+h{{k}^{2}}+2a{{k}^{2}}-8{{a}^{2}}h}{4{{a}^{2}}+{{k}^{2}}} \\\ & \Rightarrow x=\dfrac{h{{k}^{2}}+2a{{k}^{2}}-4{{a}^{2}}h}{4{{a}^{2}}+{{k}^{2}}} \\\ \end{aligned}$$ Similarly, we get the $$'y'$$ co – ordinate of $$'T'$$ as $$\begin{aligned} & \Rightarrow \dfrac{y-k}{-k}=\dfrac{{{k}^{2}}-4ah}{4{{a}^{2}}+{{k}^{2}}} \\\ & \Rightarrow y=k+\dfrac{-{{k}^{3}}+4ahk}{4{{a}^{2}}+{{k}^{2}}} \\\ \end{aligned}$$ By doing the LCM and adding the terms we get $$\begin{aligned} & \Rightarrow y=\dfrac{4{{a}^{2}}k+{{k}^{3}}-{{k}^{3}}+4ahk}{4{{a}^{2}}+{{k}^{2}}} \\\ & \Rightarrow y=\dfrac{4ak\left( h+a \right)}{4{{a}^{2}}+{{k}^{2}}} \\\ \end{aligned}$$ Therefore, the co – ordinates of point $$'T'$$ are $$\Rightarrow T=\left( \dfrac{h{{k}^{2}}+2a{{k}^{2}}-4{{a}^{2}}h}{4{{a}^{2}}+{{k}^{2}}},\dfrac{4ak\left( h+a \right)}{4{{a}^{2}}+{{k}^{2}}} \right)$$ Let us find the length of ‘ST’ using the distance formula We know that the formula of distance between $$\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$$ is given as $$ST=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$$ By using the above formula we get $$\begin{aligned} & \Rightarrow ST=\sqrt{{{\left( \dfrac{h{{k}^{2}}+2a{{k}^{2}}-4{{a}^{2}}h}{4{{a}^{2}}+{{k}^{2}}}-a \right)}^{2}}+{{\left( \dfrac{4ak\left( h+a \right)}{4{{a}^{2}}+{{k}^{2}}} \right)}^{2}}} \\\ & \Rightarrow ST=\dfrac{1}{4{{a}^{2}}+{{k}^{2}}}\sqrt{{{\left( h{{k}^{2}}+2a{{k}^{2}}-4{{a}^{2}}h-4{{a}^{3}}-a{{k}^{2}} \right)}^{2}}+16{{a}^{2}}{{k}^{2}}{{\left( h+a \right)}^{2}}} \\\ \end{aligned}$$ By taking the common terms from the first term inside the square root we get $$\begin{aligned} & \Rightarrow ST=\dfrac{1}{4{{a}^{2}}+{{k}^{2}}}\sqrt{{{\left( k-4{{a}^{2}} \right)}^{2}}{{\left( h+a \right)}^{2}}+16{{a}^{2}}{{k}^{2}}{{\left( h+a \right)}^{2}}} \\\ & \Rightarrow ST=\dfrac{\left( h+a \right)}{4{{a}^{2}}+{{k}^{2}}}\sqrt{{{\left( k-4{{a}^{2}} \right)}^{2}}+16{{a}^{2}}{{k}^{2}}} \\\ & \Rightarrow ST=\dfrac{\left( h+a \right)}{4{{a}^{2}}+{{k}^{2}}}\left( 4{{a}^{2}}+{{k}^{2}} \right) \\\ & \Rightarrow ST=h+a \\\ \end{aligned}$$ Now let us find the distance of pint P to the directirx We know that the equation of directrix is given as $$\Rightarrow x+a=0$$ We know that formula of the distance of $$P\left( h,k \right)$$ to line $$ax+by+c=0$$ is given as $$D=\dfrac{\left| ah+bk+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$$ By using the above formula the distance of point $$P\left( h,k \right)$$ to $$x+a=0$$ is given as $$\begin{aligned} & \Rightarrow D=\dfrac{\left| h+0+a \right|}{\sqrt{{{1}^{2}}+{{0}^{2}}}} \\\ & \Rightarrow D=h+a \\\ \end{aligned}$$ Here we can see that $$\Rightarrow ST=D$$ Therefore we can say that the foot of this perpendicular from the focus is equal to distance of point P from its directrix. Hence the required result has been proved. **Note:** There is a shortcut for this solution. The foot of perpendicular of point P on its polar with respect to curve $$S\equiv {{y}^{2}}=4ax$$ will be same as P. that means in the above solution the points $$'P'$$ and $$'T'$$ will coincide. Therefore, if we can prove that $$D=SP$$ then we can easily prove the required result. By using the distance formula the length of SP is $$\Rightarrow SP=\sqrt{{{\left( h-a \right)}^{2}}+{{k}^{2}}}$$ Since point $$P\left( h,k \right)$$ lies on parabola we get $$\Rightarrow {{k}^{2}}=4ah$$ By substituting the this formula in above equation we get $$\begin{aligned} & \Rightarrow SP=\sqrt{{{\left( h-a \right)}^{2}}+4ah} \\\ & \Rightarrow SP=h+a=D \\\ \end{aligned}$$ Hence the required result has been proved.