Question
Question: If the particle moves from A to B as shown in figure, the ratio of displacement to distance covered ...
If the particle moves from A to B as shown in figure, the ratio of displacement to distance covered by particle is (If R is the radius of track)
& A)\dfrac{2\sqrt{2}}{3\pi } \\\ & B)\dfrac{3\pi }{2\sqrt{2}} \\\ & C)\dfrac{\pi }{\sqrt{2}} \\\ & D)\dfrac{\pi }{2\sqrt{2}} \\\ \end{aligned}$$ 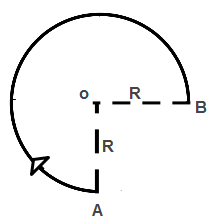Solution
In this question we have to calculate the distance and displacement. Since we know that distance is the actual path travelled while displacement is the linear path travelled from initial to final point. Distance travelled on a circle is the circumference of the circle of radius R. Here one quarter distance is subtracted from the circumference.
Complete step-by-step answer:
According to figure, particle travels from initial point A to d=final point B via a longer path of a circle of radius R.
Since we know that distance is defined as the actual path travelled by a particle on a circle of radius R.
so the distance of this motion from A to B can be calculated by subtracting a quarter distance from circumference of a circle. So distance can be expressed as-
Distance = 2πR−2πR
Distance Covered = 23πR (Equation1).
Displacement is defined as the shortest path travelled by a particle or in other words displacement is defined as linear path travelled between initial and final positions. So here in this diagram of circular motion initial point is A and final point is B. So displacement can be represented by drawing a linear path between initial point A and final point B as shown in diagram drawn below:-
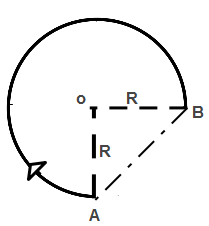
From this above displacement is represented by a linear path between AB. This can be calculated by Pythagora's theorem applied on triangle AOB.
According to Pythagoras theorem-
(Hypotenuse)2=(Perpendicular)2+(Base)2
Here Hypotenuse is side AB
Let Perpendicular is side AO and Base is side BO.
Perpendicular and base can also be interchanged, due to this no change in observed on length of side AB.
⇒AB2=AO2+BO2
⇒AB2=R2+R2
⇒AB2=2R2
∴AB=2R
So, displacement between point A and point B becomes 2R(Equation2).
According to the question we have to calculate the ratio of displacement to distance. So, we get the ratio by dividing equation and equation 1.So we get,
\Rightarrow $$$$\dfrac{Displacement}{Dis\tan ce}=\dfrac{2\sqrt{2}R}{3\pi R}
∴DistanceDisplacement=3π22
This is the required ratio of displacement and distance.
So, the correct answer is “Option A”.
Note: Distance is always greater than or equal to displacement. Displacement can be positive, negative and zero but distance is always positive if the body is moving. Displacement is the vector quantity while Distance is the scalar quantity. Distance is the actual path travelled while displacement is the shortest path travelled.
