Question
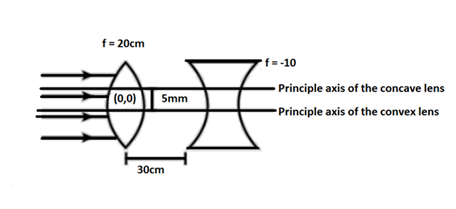
Question: If the optical center of the convex and the concave lenses are separated by a distance 5mm as shown ...
If the optical center of the convex and the concave lenses are separated by a distance 5mm as shown in the figure. Find the coordinate of the final image formed by the combination of if a parallel beam of light is incident on lenses. Origin is at the optical center of the convex lens.
A. 25cm, 0.5cm
B. 25cm, 0.25cm
C. 25cm, -0.5cm
D. 25cm, -0.25cm
Solution
When a parallel beam of light is intent on a convex lens, it will form an image on the focal point of convex lens. And this image acts as an object for the concave lens and by applying formulas for the concave lens we get the image formed by the concave lens.
Formula used:
v1−u1=f1m=uvm=h objecth image
Complete step by step solution:
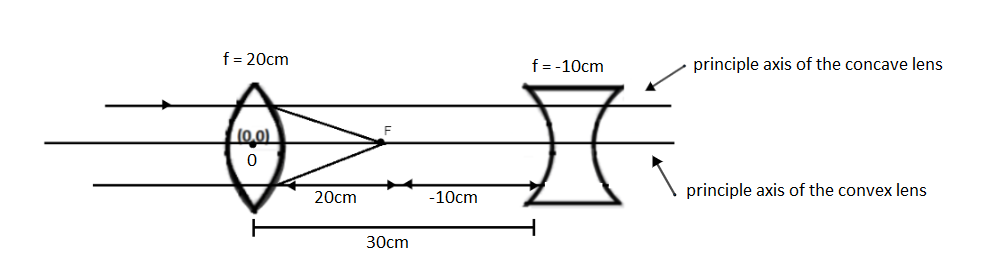
As we know that when a parallel beam of the light incident on the lens the image will form on the focal point of the convex lens.
Now the distance of the image from the origin 0 (0, 0) is
I1=20cm
And this image formed on the focal point will act as an object for the concave lens.
From the figure object distance from concave lens is,
u=−10cm
-ve sign denotes that the object is on the left side from the concave lens.
Focal point of the concave lens is given as,
f = -10cm
Now the formula for the concave lens.
v1−u1=f1....(1)
Where, v = image distance
u = object distance
f = focal point of concave lens.
Now substitute all the values in the equation (1)
⇒v1−(−10)1=−101⇒v1=10−1−101⇒v1=100−20∴v=−5cm
Now we know that magnification of the concave lens,
m=uv....(2)
Where, m = magnification
v = image distance
u = object distance
Now we also know that formula for the magnification is,
⇒m=h objecth image...(3)
Where, h image = height of the image
h object = height of the object
It is given in the question that the principal axis of the concave lens is 5mm upper than the convex lens, therefore we can say that height of the object is,
h object = 5mm = 0.5cm
From the equation (2) and equation (3)
h objecth image=uv...(4)
Now substitute all the values in the equation (4)
0.5h image=−10−5h image=0.5×0.5∴h image=0.25cm
Here the value of v = -5cm which is 25cm from the 0 (0, 0) and height is 0.25cm
Therefore correct option (b) is correct 25cm, 0.25cm.
Note:
In this question the difference between both the parallel principal axes of convex and concave lenses is 5mm, so when we are calculating the height of an image doesn’t forget to convert the unit of mm into cm.
