Question

If the number of real solution(s) of the equation $x^2 + 3x + 2 = min\{|x-3|, |x + 2|\}$ is n, then a function $f: R \rightarrow R$ defined by $f(x) = log_{\sqrt{m}}\{\sqrt{2}(sinx - cosx) + m - 2\}$, for some $m$, such that the range of $f$ is $[0, n]$, then value of $(m + n)$ is equal to

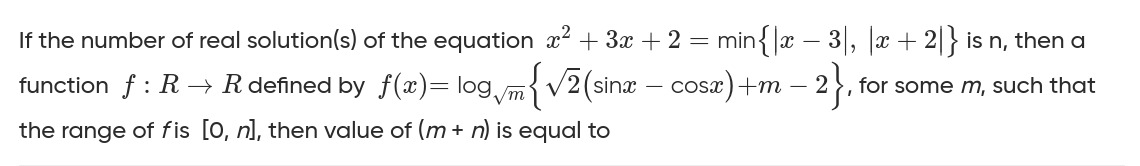
• A. 5
• B. 6
• C. 7
• D. 8

Answer 1

7

Answer 2

The problem consists of two main parts: first, finding the number of real solutions (n) for a given equation, and second, using 'n' to determine the value of 'm' from a function whose range is specified. Finally, we calculate (m+n).

Part 1: Find n

The given equation is $x^2 + 3x + 2 = \min\{|x-3|, |x+2|\}$.
Let's analyze the term $\min\{|x-3|, |x+2|\}$. The critical point where $|x-3| = |x+2|$ is found by solving $x-3 = -(x+2)$, which gives $2x=1 \implies x=1/2$.

• If $x < 1/2$: For example, if $x=0$, $|0-3|=3$ and $|0+2|=2$. So, $\min\{|x-3|, |x+2|\} = |x+2|$.
• If $x \ge 1/2$: For example, if $x=1$, $|1-3|=2$ and $|1+2|=3$. So, $\min\{|x-3|, |x+2|\} = |x-3|$.

Now we solve the equation in two cases:

Case 1: $x < 1/2$

The equation becomes $x^2 + 3x + 2 = |x+2|$.

Subcase 1.1: $-2 \le x < 1/2$ (i.e., $x+2 \ge 0$)

$x^2 + 3x + 2 = x+2$
$x^2 + 2x = 0$
$x(x+2) = 0$

This gives $x=0$ or $x=-2$. Both values satisfy the condition $-2 \le x < 1/2$. So, $x=0$ and $x=-2$ are solutions.

Subcase 1.2: $x < -2$ (i.e., $x+2 < 0$)

$x^2 + 3x + 2 = -(x+2)$
$x^2 + 3x + 2 = -x-2$
$x^2 + 4x + 4 = 0$
$(x+2)^2 = 0$

This gives $x=-2$. However, this value does not satisfy the condition $x < -2$. So, there are no solutions in this subcase.

Case 2: $x \ge 1/2$

The equation becomes $x^2 + 3x + 2 = |x-3|$.

Subcase 2.1: $1/2 \le x < 3$ (i.e., $x-3 < 0$)

$x^2 + 3x + 2 = -(x-3)$
$x^2 + 3x + 2 = -x+3$
$x^2 + 4x - 1 = 0$

Using the quadratic formula, $x = \frac{-4 \pm \sqrt{4^2 - 4(1)(-1)}}{2(1)} = \frac{-4 \pm \sqrt{16+4}}{2} = \frac{-4 \pm \sqrt{20}}{2} = -2 \pm \sqrt{5}$.
$\sqrt{5} \approx 2.236$.
$x_1 = -2 + \sqrt{5} \approx -2 + 2.236 = 0.236$. This value does not satisfy $x \ge 1/2$.
$x_2 = -2 - \sqrt{5} \approx -2 - 2.236 = -4.236$. This value does not satisfy $x \ge 1/2$.
So, there are no solutions in this subcase.

Subcase 2.2: $x \ge 3$ (i.e., $x-3 \ge 0$)

$x^2 + 3x + 2 = x-3$
$x^2 + 2x + 5 = 0$

The discriminant is $D = b^2 - 4ac = 2^2 - 4(1)(5) = 4 - 20 = -16$. Since $D < 0$, there are no real solutions in this subcase.

Combining all cases, the real solutions for the equation are $x=0$ and $x=-2$.
Therefore, the number of real solutions, $n=2$.

Part 2: Find m

The function is $f(x) = \log_{\sqrt{m}}\{\sqrt{2}(\sin x - \cos x) + m - 2\}$.
The range of $f$ is given as $[0, n]$, which is $[0, 2]$.

Let's analyze the argument of the logarithm: $Y = \sqrt{2}(\sin x - \cos x) + m - 2$.
The expression $\sin x - \cos x$ can be written as $\sqrt{2}\left(\frac{1}{\sqrt{2}}\sin x - \frac{1}{\sqrt{2}}\cos x\right) = \sqrt{2}\left(\sin x \cos\frac{\pi}{4} - \cos x \sin\frac{\pi}{4}\right) = \sqrt{2}\sin\left(x-\frac{\pi}{4}\right)$.
So, $\sqrt{2}(\sin x - \cos x) = \sqrt{2} \cdot \sqrt{2}\sin\left(x-\frac{\pi}{4}\right) = 2\sin\left(x-\frac{\pi}{4}\right)$.
The range of $2\sin\left(x-\frac{\pi}{4}\right)$ is $[-2, 2]$.
Therefore, the argument $Y$ has a range of $[-2 + m - 2, 2 + m - 2]$, which is $[m-4, m]$.

For the logarithm to be defined:

1. The base $\sqrt{m}$ must be greater than 0 and not equal to 1. This implies $m>0$ and $m \ne 1$.
2. The argument $Y$ must be positive. So, $Y > 0$. Since the minimum value of $Y$ is $m-4$, we must have $m-4 > 0 \implies m > 4$.

This condition $m>4$ automatically satisfies $m>0$ and $m \ne 1$.

Since $m>4$, the base $\sqrt{m} > \sqrt{4} = 2$. As the base is greater than 1, the logarithm function $f(x)$ is an increasing function of its argument $Y$.
Thus, the minimum value of $f(x)$ occurs when $Y$ is minimum ($m-4$), and the maximum value occurs when $Y$ is maximum ($m$).
Given range of $f(x)$ is $[0, 2]$:
$f_{min} = \log_{\sqrt{m}}(m-4) = 0$
$f_{max} = \log_{\sqrt{m}}(m) = 2$

From $f_{min} = 0$:
$\log_{\sqrt{m}}(m-4) = 0 \implies m-4 = (\sqrt{m})^0 = 1$.
$m-4 = 1 \implies m=5$.

Let's check if $m=5$ is consistent with $f_{max}=2$:
If $m=5$, then $\sqrt{m} = \sqrt{5}$.
$f_{max} = \log_{\sqrt{5}}(5)$. Since $5 = (\sqrt{5})^2$, $\log_{\sqrt{5}}(5) = 2$.
This is consistent. Also, $m=5$ satisfies $m>4$.

So, $m=5$.

Part 3: Calculate (m+n)

We found $n=2$ and $m=5$.
Therefore, $m+n = 5+2 = 7$.

The final answer is $\boxed{7}$.