Question

If the number of atoms per unit cell in hcp structure and bcc structure gets halved. Then ratio percentage voids in hcp and bcc structure is
(A) $\dfrac{34}{27}$
(B) $\dfrac{21}{22}$
(C) $\dfrac{22}{21}$
(D) $\dfrac{37}{34}$

Answer 1

By calculating the packaging efficiency of each crystal, we can find the ratio of percentage voids in hcp and bcc. The packaging efficiency is defined as the fraction of unit cells occupied by the atoms. The value must be always less than 100. Later from that value we can calculate the percentage of voids.

Complete step by step solution:
Let’s first see some of the basic things like what a unit cell is. Unit cell is defined as the smallest repeating portion of the crystal. It is the basic structural unit or building block of the crystal. Some of the common crystal structures are face centered cubic, body centered cubic and hexagonal closed packed crystal.
In hexagonal close packed structure, the number of atoms in the unit cell is given by
$N={{N}_{c}}+{{N}_{f}}+{{N}_{i}}$
Where
${{N}_{c}}$= number of atoms at the corner
${{N}_{f}}$=total number of atoms at the face-centre
${{N}_{i}}$=total number of atoms at the interior
$N=12\times \dfrac{1}{6}+2\times \dfrac{1}{2}+3\times 1$
$N=2+1+3=6$
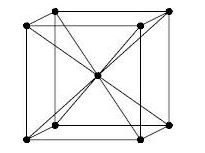
In body centered packed structure, the number of atoms in the unit cell is given by
$N={{N}_{c}}+{{N}_{b}}$
$N=8\times \dfrac{1}{8}+1\times 1$
$N=1+1=2$
In a hexagonal close packed structure, the number of atoms in the unit cell is 6.
In a body centered packed structure, the number of atoms in the unit cell is 2.
$\text{Packaging efficiency= }\dfrac{\text{Volume occupied by atom}}{\text{volume of the unit cell}}\times 100$
$\text{Packaging efficiency of hcp= }\dfrac{6\times \dfrac{4}{3}\pi {{r}^{3}}}{base\times height}\times 100$
$a=2r,\text{ c=}\sqrt{\dfrac{8}{3}}a$
$\text{Packaging efficiency of hcp= }\dfrac{6\times \dfrac{4}{3}\pi {{r}^{3}}}{3\times {{a}^{2}}\sin 60{}^\circ \times c}\times 100$
$\text{Packaging efficiency of hcp= }\dfrac{6\times \dfrac{4}{3}\pi {{r}^{3}}}{3\times \sqrt{\dfrac{3}{2}}\times \sqrt{\dfrac{8}{3}}\times {{a}^{3}}}\times 100$
$\text{Packaging efficiency of hcp= }\dfrac{8\pi {{r}^{3}}}{3\times \sqrt{\dfrac{3}{2}}\times \sqrt{\dfrac{8}{3}}\times {{(2r)}^{3}}}\times 100$
$\text{Packaging efficiency of hcp= }\dfrac{8\pi {{r}^{3}}}{3\times \sqrt{\dfrac{3}{2}}\times \sqrt{\dfrac{8}{3}}\times 8{{r}^{3}}}\times 100$
$\text{Packaging efficiency of hcp=74 }\\!\\!$, since the value is halved it will be 37%.
Percentage of voids of hcp=100-37=63%
$\text{Packaging efficiency of bcc= }\dfrac{2\times \dfrac{4}{3}\pi {{r}^{3}}}{{{a}^{3}}}\times 100$
$a=\dfrac{4r}{\sqrt{3}}$
$\text{Packaging efficiency of bcc= }\dfrac{2\times \dfrac{4}{3}\pi {{r}^{3}}}{{{(\dfrac{4r}{\sqrt{3}})}^{3}}}\times 100$
$\text{Packaging efficiency of bcc=68 }\\!\\!$, which halved to give 34%
Percentage of voids of bcc=100-34=66%
ratio percentage voids in hcp and bcc structure $\text{=}\dfrac{\text{percentage of voids of hcp}}{\text{percentage of voids of bcc}}$
ratio percentage voids in hcp and bcc structure $\text{=}\dfrac{63}{66}$
ratio percentage voids in hcp and bcc structure $\text{=}\dfrac{21}{22}$

Therefore, the correct answer is option(B) $\dfrac{21}{22}$.

Additional information:
Hexagonal close packed structure
In a hexagonal closed packed structure, there are atoms at each corner of the hexagon i.e. one atom at each of the 12 corners, one atom at the center of each two faces in the hexagon i.e. two atoms at top and bottom faces. and each atom at the line which connects the perpendicular i.e. 3 atoms in between top and bottom faces.

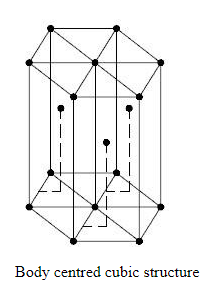
In a body centered cubic crystal, there are atoms at each corner of the cube, i.e one atom at each of the 8 corners and one atom at the center of the body of the cube.

Note: The packaging efficiency value must be always less than 100. In order to obtain the percentage of voids i.e. empty space, you must be subtracting the value of percentage efficiency value of the unit cell by 100