Question

If the normals at $P$ and $Q$ meet on the parabola, prove that the point of intersection of the tangents at $P$ and $Q$ lies either on a straight line, which is parallel to tangent at vertex or on the curve whose equation is ${{y}^{2}}\left( x+2a \right)+4{{a}^{3}}=0$.

Answer 1

Hint: The general equation of normal to the parabola at a point $\left( a{{t}^{2}},2at \right)$ is given by $y=-tx+2at+a{{t}^{3}}$, where $t$ is a parameter.
The equation of tangent at $\left( a{{t}^{2}},2at \right)$ is given by $ty=x+a{{t}^{2}}$, where $t$ is a parameter.

Complete step-by-step answer:

We will consider the equation of the parabola to be ${{y}^{2}}=4ax$.

Now , we will consider two points on the parabola given by $P\left( at_{1}^{2},2a{{t}_{1}} \right)$and $Q\left( at_{2}^{2},2a{{t}_{2}} \right)$ , where ${{t}_{1}}$ and ${{t}_{2}}$ are parameters.

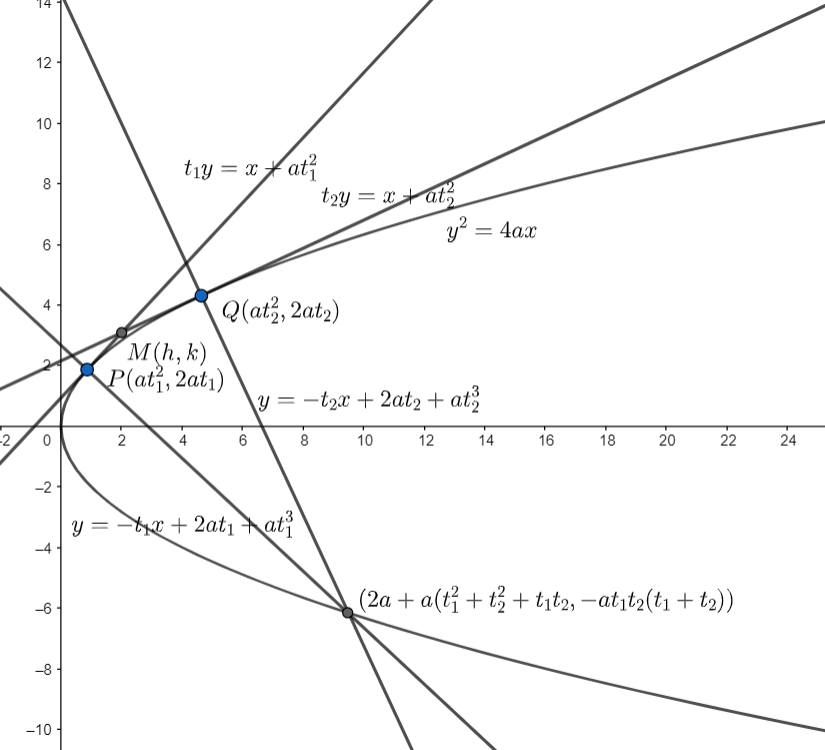
Now, we need to find the equation of normal at $P$ and $Q$.

We know, the general equation of normal to the parabola at a point $\left( a{{t}^{2}},2at \right)$is given by $y=-tx+2at+a{{t}^{3}}$, where $t$ is a parameter.

So, the normal to the parabola at point $P\left( at_{1}^{2},2a{{t}_{1}} \right)$ will be given is given by substituting ${{t}_{1}}$ in place of $t$ in the general equation of normal.

On substituting ${{t}_{1}}$ in place of $t$ in the general equation of normal , we get
$y=-{{t}_{1}}x+2a{{t}_{1}}+at_{1}^{3}....\left( i \right)$

And the normal to the parabola at point $Q\left( at_{2}^{2},2a{{t}_{2}} \right)$ is given as
$y=-{{t}_{2}}x+2a{{t}_{2}}+at_{2}^{3}....\left( ii \right)$

Now, to find the point of intersection of $\left( i \right)$ and $\left( ii \right)$, we substitute the value of $y$ from equation $\left( i \right)$ in equation $\left( ii \right)$.

On substituting the value of $y$ from equation $\left( i \right)$ in equation $\left( ii \right)$, we get
$-{{t}_{1}}x+2a{{t}_{1}}+at_{1}^{3}=-{{t}_{2}}x+2a{{t}_{2}}+at_{2}^{3}$
$\Rightarrow \left( {{t}_{2}}-{{t}_{1}} \right)x=2a\left( {{t}_{2}}-{{t}_{1}} \right)+a\left( t_{2}^{3}-t_{1}^{3} \right)$
$\Rightarrow \left( {{t}_{2}}-{{t}_{1}} \right)x=2a\left( {{t}_{2}}-{{t}_{1}} \right)+a\left( {{t}_{2}}-{{t}_{1}} \right)\left( t_{1}^{2}+t_{2}^{2}+{{t}_{1}}{{t}_{2}} \right)$
$\Rightarrow x=2a+a\left( t_{1}^{2}+t_{2}^{2}+{{t}_{1}}{{t}_{2}} \right)$

Now, we will substitute $x=2a+a\left( t_{1}^{2}+t_{2}^{2}+{{t}_{1}}{{t}_{2}} \right)$ in equation $\left( i \right)$.

On substituting $x=2a+a\left( t_{1}^{2}+t_{2}^{2}+{{t}_{1}}{{t}_{2}} \right)$ in equation $\left( i \right)$, we get
$y=-{{t}_{1}}\left( 2a+a\left( t_{1}^{2}+t_{2}^{2}+{{t}_{1}}{{t}_{2}} \right) \right)+2a{{t}_{1}}+at_{1}^{3}$
$=-2a{{t}_{1}}-at_{1}^{3}-at_{2}^{2}{{t}_{1}}-at_{1}^{2}{{t}_{2}}+2a{{t}_{1}}+at_{1}^{3}$
$\Rightarrow y=-a{{t}_{1}}{{t}_{2}}\left( {{t}_{1}}+{{t}_{2}} \right)$

So, the point of intersection of the normal is
$\left( 2a+a\left( t_{1}^{2}+t_{2}^{2}+{{t}_{1}}{{t}_{2}} \right),-a{{t}_{1}}{{t}_{2}}\left( {{t}_{1}}+{{t}_{2}} \right) \right)$

Now, this point lies on the parabola . So , $\left( 2a+a\left( t_{1}^{2}+t_{2}^{2}+{{t}_{1}}{{t}_{2}} \right),-a{{t}_{1}}{{t}_{2}}\left( {{t}_{1}}+{{t}_{2}} \right) \right)$ must satisfy the equation of the parabola.

So, ${{\left[ -a{{t}_{1}}{{t}_{2}}\left( {{t}_{1}}+{{t}_{2}} \right) \right]}^{2}}=4a\left( 2a+a\left( t_{1}^{2}+t_{2}^{2}+{{t}_{1}}{{t}_{2}} \right) \right).....\left( iii \right)$

Now, we know the equation of tangent at $\left( a{{t}^{2}},2at \right)$ is given by $ty=x+a{{t}^{2}}$, where $t$ is a parameter.

So, the equation of tangent at $P\left( at_{1}^{2},2a{{t}_{1}} \right)$ is given by
${{t}_{1}}y=x+at_{1}^{2}......(iv)$

And the equation of tangent at $Q\left( at_{2}^{2},2a{{t}_{2}} \right)$ is given by
${{t}_{2}}y=x+at_{2}^{2}......(v)$

Now , let the point of intersection of these tangents be $M\left( h,k \right)$.

Now, from equation $\left( iv \right)$, we have
$y{{t}_{1}}=x+at_{1}^{2}$
$\Rightarrow x={{t}_{1}}\left( y-a{{t}_{1}} \right).....\left( vi \right)$
We will substitute the value of $x$ from equation $(vi)$ in equation $\left( v \right)$.

On substituting value of $x$ from equation$(vi)$ in equation $\left( v \right)$, we get,
$y{{t}_{2}}={{t}_{1}}y-at_{1}^{2}+at_{2}^{2}$
$\Rightarrow y\left( {{t}_{2}}-{{t}_{1}} \right)=a\left( t_{2}^{2}-t_{1}^{2} \right)$
$\Rightarrow y=a\left( {{t}_{1}}+{{t}_{2}} \right)$

Substituting $y=a\left( {{t}_{1}}+{{t}_{2}} \right)$ in $\left( vi \right)$, we get
$x={{t}_{1}}\left( a{{t}_{1}}+a{{t}_{2}}-a{{t}_{1}} \right)$
$\Rightarrow x=a\left( {{t}_{1}}{{t}_{2}} \right)$

So, the point of intersection of tangents $\left( iv \right)$ and $\left( v \right)$ is $\left( a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right)$.

Comparing with $M\left( h,k \right)$, we get
$h=a{{t}_{1}}{{t}_{2}},k=a\left( {{t}_{1}}+{{t}_{2}} \right)$

Now, from equation $\left( iii \right)$, we have
${{\left( a{{t}_{1}}{{t}_{2}} \right)}^{2}}{{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}=4a\left( 2a+a\left( {{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}-{{t}_{1}}{{t}_{2}} \right) \right)....\left( vii \right)$

Substituting $a{{t}_{1}}{{t}_{2}}=h$and $a\left( {{t}_{1}}+{{t}_{2}}=k \right)$ in $\left( vii \right)$, we get
$\left( {{h}^{2}} \right).{{\left( \dfrac{k}{a} \right)}^{2}}=4a\left( 2a+a\left( {{\left( \dfrac{k}{a} \right)}^{2}}-\dfrac{h}{a} \right) \right)$
$\Rightarrow \dfrac{{{h}^{2}}{{k}^{2}}}{{{a}^{2}}}=8{{a}^{2}}+4{{k}^{2}}-4ah$
$\Rightarrow {{h}^{2}}{{k}^{2}}=8{{a}^{4}}+4{{a}^{2}}{{k}^{2}}-4{{a}^{3}}h$
$\Rightarrow {{k}^{2}}\left( {{h}^{2}}-4{{a}^{2}} \right)=8{{a}^{3}}\left( a-\dfrac{h}{2} \right)$
$\Rightarrow {{k}^{2}}\left( h+2a \right)\left( h-2a \right)=4{{a}^{3}}\left( 2a-h \right)$
$\Rightarrow \left( h-2a \right)\left( {{k}^{2}}\left( h+2a \right)+4{{a}^{3}} \right)=0.....(viii)$

Now, to find the locus of $M\left( h,k \right)$, we will substitute $(x,y)$ in place of $(h,k)$ in equation $(viii)$.

So , the locus of $M\left( h,k \right)$ is given as
$\left( x-2a \right)\left( {{y}^{2}}\left( x+2a \right)+4{{a}^{3}} \right)=0$
So , either $x=2a$or $\left( {{y}^{2}}\left( x+2a \right)+4{{a}^{3}} \right)=0$

Hence , the point of intersection lies either on a straight line parallel to the tangent to vertex or on the curve $\left( {{y}^{2}}\left( x+2a \right)+4{{a}^{3}} \right)=0$.

Note: While simplifying the equations, please make sure that sign mistakes do not occur. These mistakes are very common and can cause confusions while solving. Ultimately the answer becomes wrong. So, sign conventions should be carefully taken .