Question

If the normal at P ‘t’ on ${{y}^{2}}=4ax$ meets the curve again at Q, the point on the curve, the normal at which also passes through Q has coordinates(......,......).
A. $\left( \dfrac{2a}{{{t}^{2}}},\dfrac{2a}{t} \right)$
B. $\left( \dfrac{4a}{{{t}^{2}}},\dfrac{2a}{t} \right)$
C. $\left( \dfrac{4a}{{{t}^{2}}},\dfrac{4a}{t} \right)$
D. $\left( \dfrac{4a}{{{t}^{2}}},\dfrac{8a}{t} \right)$

Answer 1

Here, we will assume the required point to be R. We will take the parameters of point Q and R as ${{t}_{1}}$ and ${{t}_{2}}$ respectively. Then, we will calculate the equation of the normal at P in which we will calculate the slope by finding ${{\left( -\dfrac{dx}{dy} \right)}_{\left( {{x}_{1}},{{y}_{1}} \right)}}$ at point P and then taking the general equation of a line $y-k=m\left( x-h \right)$ where ‘m’ is the slope and (h,k) are fixed points on the line which we will take as the point P. after that, we will solve this with the parabola ${{y}^{2}}=4ax$ which will give us the relation between the parameters of Q and P, i.e. ${{t}_{1}}$ and $t$. Then using the formula ${{\left( -\dfrac{dx}{dy} \right)}_{\left( {{x}_{1}},{{y}_{1}} \right)}}$ we will find the slope of the normal at point R and using the abovementioned general equation, find the equation of the normal where we will take the fixed point (h,k) as Q. Then we will obtain the equation of normal in terms of ${{t}_{1}}$ and ${{t}_{2}}$. Then we will put $t$ in terms of ${{t}_{1}}$ in that equation from the relation we obtained. Thus, our normal will now be in the form of $t$ and ${{t}_{2}}$ and then we will put the coordinates given in the options one by one (in which we will obtain the value of ${{t}_{2}}$ by equating the coordinates in the given options with the parametric coordinates of point R) and the option which will satisfy the equation will be our required answer.

Complete step-by-step solution
Now, we have been given that P is a point on the parabola ${{y}^{2}}=4ax$ with the parameter ‘t’.
Thus, we can say the coordinates of point P are $\left( a{{t}^{2}},2at \right)$ .
In the below figure, we have shown the parabola ${{y}^{2}}=4ax$ with two normals passing through point P and R respectively and both the normals are passing through the same point i.e. Q.

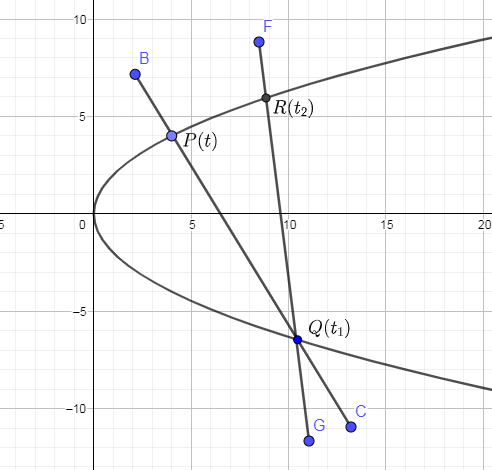
In the above figure, we have also shown that the parametric coordinates of P with “t” and R and Q with ${{t}_{2}}\And {{t}_{1}}$ respectively.
Now, we know that the slope of the normal at any point on a curve is given by ${{\left( -\dfrac{dx}{dy} \right)}_{\left( {{x}_{1}},{{y}_{1}} \right)}}$ where $\left( {{x}_{1}},{{y}_{1}} \right)$ is the point on the curve on which the normal is incident.
Here that point is point P. Thus, we can say that:
$\left( {{x}_{1}},{{y}_{1}} \right)=\left( a{{t}^{2}},2at \right)$
Now, for finding the slope of the normal, we first need to find the value of $\dfrac{dx}{dy}$ .
We have been given the equation of the curve as ${{y}^{2}}=4ax$
Differentiating both sides with respect to x we get:
$\begin{aligned} & {{y}^{2}}=4ax \\\ & \Rightarrow 2y.\dfrac{dy}{dx}=4a \\\ & \Rightarrow \dfrac{dy}{dx}=\dfrac{4a}{2y} \\\ & \Rightarrow \dfrac{dy}{dx}=\dfrac{2a}{y} \\\ & \Rightarrow \dfrac{dx}{dy}=\dfrac{y}{2a} \\\ & \Rightarrow -\dfrac{dx}{dy}=-\dfrac{y}{2a} \\\ \end{aligned}$
Now, by putting the coordinates of P, we will get the slope of the normal.
Let the slope of the normal at P be ‘m’.
Thus, the value of m is given as:
$\begin{aligned} & m={{\left( -\dfrac{y}{2a} \right)}_{\left( a{{t}^{2}},2at \right)}} \\\ & \Rightarrow m=-\dfrac{2at}{2a} \\\ & \Rightarrow m=-t \\\ \end{aligned}$
Thus, the slope of the normal is ‘-t’.
Now, we will find the equation of the normal at point P.
We know that the equation of a line having slope ‘m’ and passing through (h,k) is given as:
$y-k=m\left( x-h \right)$
Here, (h,k) are the coordinates of point P and $m=-t$ .
Thus, putting in these values, we get our equation as:
$\begin{aligned} & y-2at=-t\left( x-a{{t}^{2}} \right) \\\ & \Rightarrow y-2at=-tx+a{{t}^{3}} \\\ \end{aligned}$
$\Rightarrow tx+y=a{{t}^{3}}+2at$
Now, we have been given that the normal also passes through the point Q on the same parabola.
Let the parameter of point Q be $'{{t}_{1}}'$ .
Thus, the coordinates of point Q are $\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$ .
Since, the normal also passes through the point Q, its coordinates will satisfy the equation of the normal. Putting the value of the coordinates of point Q in the parabola will give us the relation between the points P and Q.
Putting the coordinates of point Q in the equation of the normal we get:
$\begin{aligned} & tx+y=a{{t}^{3}}+2at \\\ & \Rightarrow t\left( a{{t}_{1}}^{2} \right)+2a{{t}_{1}}=a{{t}^{3}}+2at \\\ & \Rightarrow at{{t}_{1}}^{2}+2a{{t}_{1}}=a{{t}^{3}}+2at \\\ & \Rightarrow a\left( t{{t}_{1}}^{2}+2{{t}_{1}} \right)=a\left( {{t}^{3}}+2t \right) \\\ & \Rightarrow t{{t}_{1}}^{2}+2{{t}_{1}}={{t}^{3}}+2t \\\ & \Rightarrow \left( t{{t}_{1}}^{2}+2{{t}_{1}} \right)-\left( {{t}^{3}}+2t \right)=0 \\\ \end{aligned}$
$\begin{aligned} & \Rightarrow \left( t{{t}_{1}}^{2}-{{t}^{3}} \right)+\left( 2{{t}_{1}}-2t \right)=0 \\\ & \Rightarrow t\left( {{t}_{1}}^{2}-{{t}^{2}} \right)+2\left( {{t}_{1}}-t \right)=0 \\\ & \Rightarrow t\left( {{t}_{1}}-t \right)\left( {{t}_{1}}+t \right)+2\left( {{t}_{1}}-t \right)=0 \\\ & \Rightarrow \left( {{t}_{1}}-t \right)\left( t\left( {{t}_{1}}+t \right)+2 \right)=0 \\\ & \text{Since }{{t}_{1}}\ne t,\text{ we can say:} \\\ & t\left( {{t}_{1}}+t \right)+2=0 \\\ & \Rightarrow t\left( {{t}_{1}}+t \right)=-2 \\\ & \Rightarrow {{t}_{1}}+t=-\dfrac{2}{t} \\\ & \Rightarrow {{t}_{1}}=-t-\dfrac{2}{t} \\\ \end{aligned}$
This gives us the required relation between them points P and Q.
Now, we have to find a point on the parabola the normal on which also passes through the point Q.
So, let us assume that that point is R and its parameter is $'{{t}_{2}}'$ .
Thus, the coordinates of point R are $\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$.
Now, the slope of the normal at R is given as:
$\begin{aligned} & {{\left( -\dfrac{dx}{dy} \right)}_{\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)}} \\\ & \Rightarrow {{\left( -\dfrac{y}{2a} \right)}_{\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)}} \\\ & \Rightarrow \left( -\dfrac{2a{{t}_{2}}}{2a} \right) \\\ & \Rightarrow -{{t}_{2}} \\\ \end{aligned}$
Thus, the slope of normal at R is $'-{{t}_{2}}'$ .
Now, to form the equation of the normal through R, we need a point the normal passes through. Since, R is unknown, we will take Q as that point.
Thus, the equation of the normal at R passing through Q is given as:
$\begin{aligned} & y-2a{{t}_{1}}=-{{t}_{2}}\left( x-a{{t}_{1}}^{2} \right) \\\ & \Rightarrow y-2a{{t}_{1}}=-{{t}_{2}}x+a{{t}_{1}}^{2}{{t}_{2}} \\\ & \Rightarrow {{t}_{2}}x+y=2a{{t}_{1}}+a{{t}_{1}}^{2}{{t}_{2}} \\\ \end{aligned}$
Putting the value of ${{t}_{2}}$ in the obtained equation of the normal we get:
$\begin{aligned} & {{t}_{2}}x+y=2a{{t}_{1}}+a{{t}_{1}}^{2}{{t}_{2}} \\\ & \Rightarrow {{t}_{2}}x+y=2a\left( -t-\dfrac{2}{t} \right)+a{{t}_{2}}{{\left( -t-\dfrac{2}{t} \right)}^{2}} \\\ & \Rightarrow {{t}_{2}}x+y=2a\left( -t-\dfrac{2}{t} \right)+a{{t}_{2}}\left( {{t}^{2}}+\dfrac{4}{{{t}^{2}}}+4 \right) \\\ \end{aligned}$
This is our required equation of the normal at R.
Now, we will check the options one by one by putting them into the equation of normal at R. The option which will satisfy the equation will be our answer.
Checking for option (A):
The given point is $\left( \dfrac{2a}{{{t}^{2}}},\dfrac{2a}{t} \right)$ .
Now, we will first put this point in the equation of the parabola to see if it satisfies the equation of the parabola or not. If it does not, there is no need to check it in the equation of the parabola as the required point R lies on the parabola.
Putting this point in the equation of the parabola we get:

& {{y}^{2}}=4ax \\\ & \Rightarrow {{\left( \dfrac{2a}{t} \right)}^{2}}=4a\left( \dfrac{2a}{{{t}^{2}}} \right) \\\ & \Rightarrow \dfrac{4{{a}^{2}}}{{{t}^{2}}}\ne \dfrac{8{{a}^{2}}}{{{t}^{2}}} \\\ \end{aligned}$$ Thus, this point does not satisfy the equation of the parabola. Hence, option (A) is the wrong answer. Checking for option (B): Putting the coordinates in option (B) in the equation of the parabola we get: $$\begin{aligned} & {{y}^{2}}=4ax \\\ & \Rightarrow {{\left( \dfrac{2a}{t} \right)}^{2}}=4a\left( \dfrac{4a}{{{t}^{2}}} \right) \\\ & \Rightarrow \dfrac{4{{a}^{2}}}{{{t}^{2}}}\ne \dfrac{16{{a}^{2}}}{{{t}^{2}}} \\\ \end{aligned}$$ Thus, this point does not satisfy the equation of the parabola. Hence, option (B) is the wrong answer. Checking for option (B): Putting the coordinates in option (C) in the equation of the parabola we get: $$\begin{aligned} & {{y}^{2}}=4ax \\\ & \Rightarrow {{\left( \dfrac{4a}{t} \right)}^{2}}=4a\left( \dfrac{4a}{{{t}^{2}}} \right) \\\ & \Rightarrow \dfrac{16{{a}^{2}}}{{{t}^{2}}}=\dfrac{16{{a}^{2}}}{{{t}^{2}}} \\\ \end{aligned}$$ Thus, this point satisfies the equation of the parabola. So we can check it for the normal. Now, the coordinates of point R in option (C) are given to us as $\left( \dfrac{4a}{{{t}^{2}}},\dfrac{4a}{t} \right)$. Now, the point R is $\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$. Thus, if we equate any of the coordinates then we will get the value of ${{t}_{2}}$. Thus, by equating the y-coordinate, we get: $\begin{aligned} & 2a{{t}_{2}}=\dfrac{4a}{t} \\\ & \Rightarrow {{t}_{2}}=\dfrac{2}{t} \\\ \end{aligned}$ Now, putting this value of ${{t}_{2}}$ and the coordinates in option (C) in the LHS of the normal obtained, we get: $$\begin{aligned} & LHS={{t}_{2}}x+y \\\ & \Rightarrow LHS=\dfrac{2}{t}\left( \dfrac{4a}{{{t}^{2}}} \right)+\dfrac{4a}{t} \\\ & \Rightarrow LHS=\dfrac{8a}{{{t}^{3}}}+\dfrac{4a}{t} \\\ \end{aligned}$$ Now, doing the same in RHS of the normal obtained, we get: $\begin{aligned} & RHS=2a\left( -t-\dfrac{2}{t} \right)+a{{t}_{2}}\left( {{t}^{2}}+\dfrac{4}{{{t}^{2}}}+4 \right) \\\ & \Rightarrow RHS=2a\left( -t-\dfrac{2}{t} \right)+a\left( \dfrac{2}{t} \right)\left( {{t}^{2}}+\dfrac{4}{{{t}^{2}}}+4 \right) \\\ & \Rightarrow RHS=-2at-\dfrac{4a}{t}+2at+\dfrac{8a}{{{t}^{3}}}+\dfrac{8a}{t} \\\ & \Rightarrow RHS=\dfrac{8a}{{{t}^{3}}}+\dfrac{4a}{t} \\\ \end{aligned}$ We can see that LHS=RHS. Hence, option (C) satisfies the equation of the normal. **Hence, option (C) is the correct option.** **Note:** Here, we have obtained a relation between $t$ and ${{t}_{1}}$ but this relation is always true for all types of parabola. So we need not derive it again and again in every question. We can directly use it as an identity. Also, we have here put all the coordinates given in the options in the equation of the parabola first and then in that of the normal. In competitive examinations, this should be our first step of the question so that we eliminate the options. In this question, if we do so, we’ll see that no option except for option (C) satisfies the equation of the parabola and hence it will be the correct answer. It will save us a valuable amount of time.