Question

If the normal at $\left( c{{t}_{1}},\dfrac{c}{{{t}_{1}}} \right)$ on the hyperbola $xy={{c}^{2}}$ cuts the hyperbola again at $\left( c{{t}_{2}},\dfrac{c}{{{t}_{2}}} \right)$, then $t_{1}^{3}{{t}_{2}}$=
(a) 2
(b) –2
(c) –1
(d) 1

Answer 1

We start solving the problem by finding the slope of the tangent using the fact that slope of the tangent at point $\left( {{x}_{1}},{{y}_{1}} \right)$ is defined as ${{\left. \dfrac{dy}{dx} \right|}_{\left( {{x}_{1}},{{y}_{1}} \right)}}$. We then find the slope of the normal using the facts that the tangent and normal of a conic are perpendicular to each other and the product of slopes of perpendicular lines is –1. We then find the equation of the normal using the given slope and point $\left( c{{t}_{1}},\dfrac{c}{{{t}_{1}}} \right)$ and then we substitute the point $\left( c{{t}_{2}},\dfrac{c}{{{t}_{2}}} \right)$ in the equations and make necessary calculations to get the required value.

Complete step by step answer:
According to the problem, we are given that the normal at $\left( c{{t}_{1}},\dfrac{c}{{{t}_{1}}} \right)$ on the hyperbola $xy={{c}^{2}}$ cuts the hyperbola again at $\left( c{{t}_{2}},\dfrac{c}{{{t}_{2}}} \right)$. We need to find the value of $t_{1}^{3}{{t}_{2}}$.

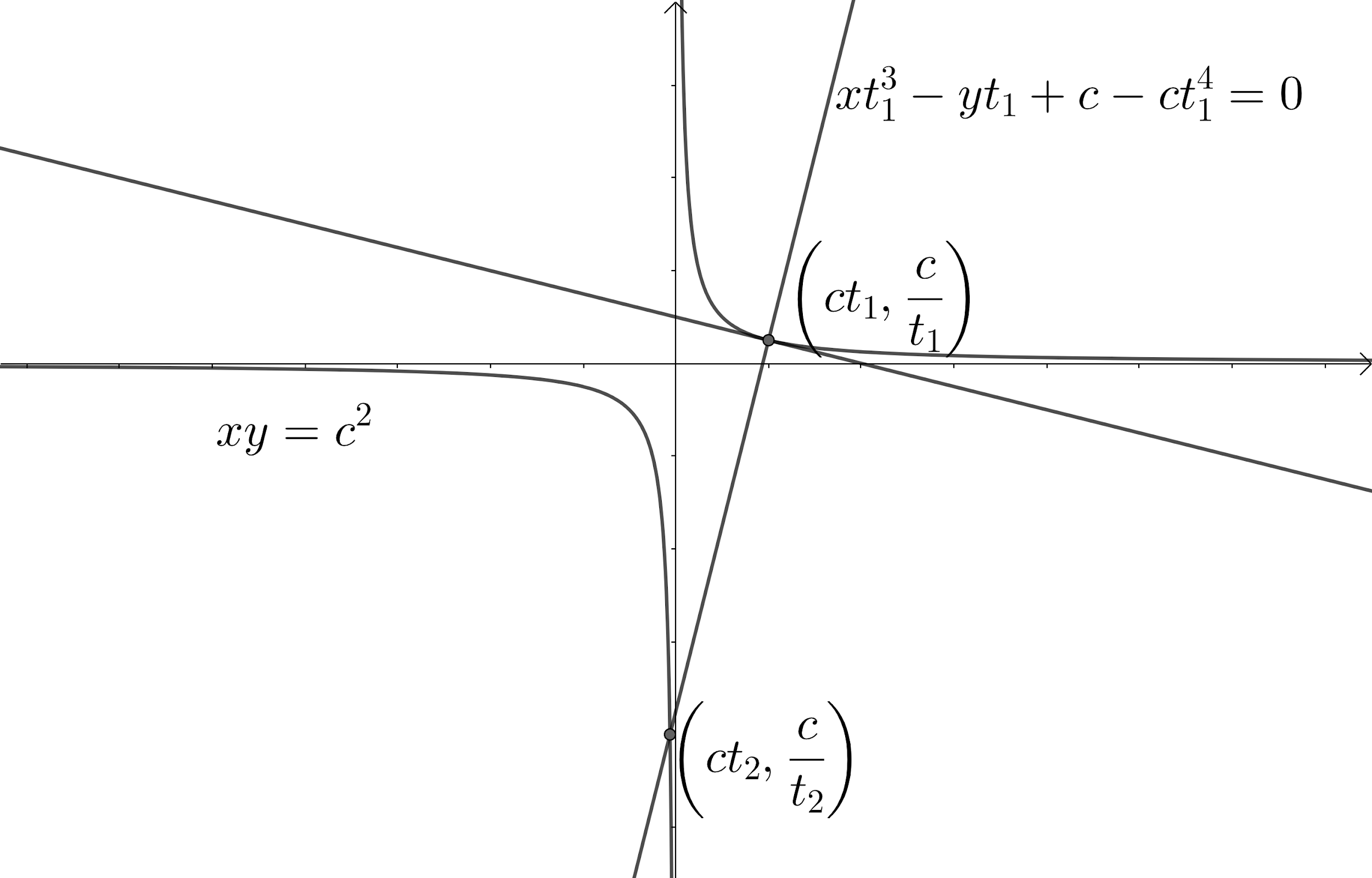
Let us first find the slope of the tangent at the point $\left( c{{t}_{1}},\dfrac{c}{{{t}_{1}}} \right)$. We know that the slope of the tangent at point $\left( {{x}_{1}},{{y}_{1}} \right)$ is defined as ${{\left. \dfrac{dy}{dx} \right|}_{\left( {{x}_{1}},{{y}_{1}} \right)}}$.
Let us differentiate both sides of $xy={{c}^{2}}$ with respect to ‘x’.
So, we have $\dfrac{d}{dx}\left( xy \right)=\dfrac{d}{dx}\left( {{c}^{2}} \right)$.
We know that $\dfrac{d}{dx}\left( uv \right)=u\dfrac{dv}{dx}+v\dfrac{du}{dx}$ and differentiation of a constant is zero.
$\Rightarrow x\dfrac{dy}{dx}+y\dfrac{dx}{dx}=0$.
We know that $\dfrac{dx}{dx}=1$.
$\Rightarrow x\dfrac{dy}{dx}+y=0$.
$\Rightarrow \dfrac{dy}{dx}=\dfrac{-y}{x}$.
Let us find the slope of tangent at the point $\left( c{{t}_{1}},\dfrac{c}{{{t}_{1}}} \right)$.
$\Rightarrow {{\left. \dfrac{dy}{dx} \right|}_{\left( c{{t}_{1}},\dfrac{c}{{{t}_{1}}} \right)}}=\dfrac{-\dfrac{c}{{{t}_{1}}}}{c{{t}_{1}}}$.
$\Rightarrow {{\left. \dfrac{dy}{dx} \right|}_{\left( c{{t}_{1}},\dfrac{c}{{{t}_{1}}} \right)}}=-\dfrac{1}{t_{1}^{2}}$.
We know that the tangent and normal of a conic are perpendicular to each other. We know that the product of slopes of tangent and normal is –1. Let us assume the slope of normal be m.
So, we get $\dfrac{-1}{t_{1}^{2}}\times m=-1$.
$\Rightarrow m=t_{1}^{2}$.
Now, let us find the equation of the normal.
We know that the equation of the line passing through the point $\left( {{x}_{1}},{{y}_{1}} \right)$ having slope m is $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$.
So, the equation of the normal is $y-\dfrac{c}{{{t}_{1}}}=t_{1}^{2}\left( x-c{{t}_{1}} \right)$.
$\Rightarrow \dfrac{y{{t}_{1}}-c}{{{t}_{1}}}=xt_{1}^{2}-ct_{1}^{3}$.
$\Rightarrow y{{t}_{1}}-c=xt_{1}^{3}-ct_{1}^{4}$.
$=xt_{1}^{3}-y{{t}_{1}}+c-ct_{1}^{4}=0$.
Now, this line passes through the point $\left( c{{t}_{2}},\dfrac{c}{{{t}_{2}}} \right)$.
So, we get $c{{t}_{2}}t_{1}^{3}-\dfrac{c}{{{t}_{2}}}\times {{t}_{1}}+c-ct_{1}^{4}=0$.
$\Rightarrow ct_{2}^{2}t_{1}^{3}-c{{t}_{1}}+c{{t}_{2}}-c{{t}_{2}}t_{1}^{4}=0$.
$\Rightarrow t_{2}^{2}t_{1}^{3}-{{t}_{2}}t_{1}^{4}+{{t}_{2}}-{{t}_{1}}=0$.
$\Rightarrow {{t}_{2}}t_{1}^{3}\left( {{t}_{2}}-{{t}_{1}} \right)+1\left( {{t}_{2}}-{{t}_{1}} \right)=0$.
$\Rightarrow \left( {{t}_{2}}t_{1}^{3}+1 \right)\left( {{t}_{2}}-{{t}_{1}} \right)=0$.
$\Rightarrow {{t}_{2}}t_{1}^{3}+1=0$ or ${{t}_{2}}-{{t}_{1}}=0$.
We know that ${{t}_{2}}\ne {{t}_{1}}$, as the given points are distinct. So, ${{t}_{2}}-{{t}_{1}}\ne 0$.
$\Rightarrow {{t}_{2}}t_{1}^{3}=-1$.
So, we have found the value of ${{t}_{2}}t_{1}^{3}$ as –1.

So, the correct answer is “Option C”.

Note: We can see that the given problem involves a heavy amount of calculations, so we need to perform every step carefully in order to avoid confusion and calculation mistakes. We should know that the two given points are not identical which is very important to remember while solving this problem. We should not randomly assume the values for ${{t}_{1}}$ and ${{t}_{2}}$ as this will not satisfy our requirements. Similarly, we can expect problems involving tangents.