Question

If the normal at $(ct,\dfrac{c}{t})$on the curve $xy={{c}^{2}}$ meets the curve again at ${{t}^{'}}$ , then
A. ${{t}^{'}}=\dfrac{-1}{{{t}^{3}}}$
B. ${{t}^{'}}=\dfrac{-1}{t}$
C. ${{t}^{'}}=\dfrac{1}{{{t}^{2}}}$
D. ${{({{t}^{'}})}^{2}}=\dfrac{-1}{{{t}^{2}}}$

Answer 1

First we will calculate the normal slope at point $(ct,\dfrac{c}{t})$ on curve $xy={{c}^{2}}$ by calculating $\dfrac{dy}{dx}$and then as we know slope of normal is $\dfrac{-dx}{dy}$ , now we can write equation of normal by using formula $y-{{y}_{1}}=(x-{{x}_{1}})m$ , now we know that it passes through point $(c{{t}^{'}},\dfrac{c}{{{t}^{'}}})$ so we will put this point in equation and get the desired result

Complete step-by-step solution:
We are given a curve $xy={{c}^{2}}$ and normal at point $(ct,\dfrac{c}{t})$ meets the curve again at $(c{{t}^{'}},\dfrac{c}{{{t}^{'}}})$ . In the below, we have drawn a hyperbola $xy={{c}^{2}}$ and also draw a tangent and normal at point $(ct,\dfrac{c}{t})$ meets the curve again at $(c{{t}^{'}},\dfrac{c}{{{t}^{'}}})$.

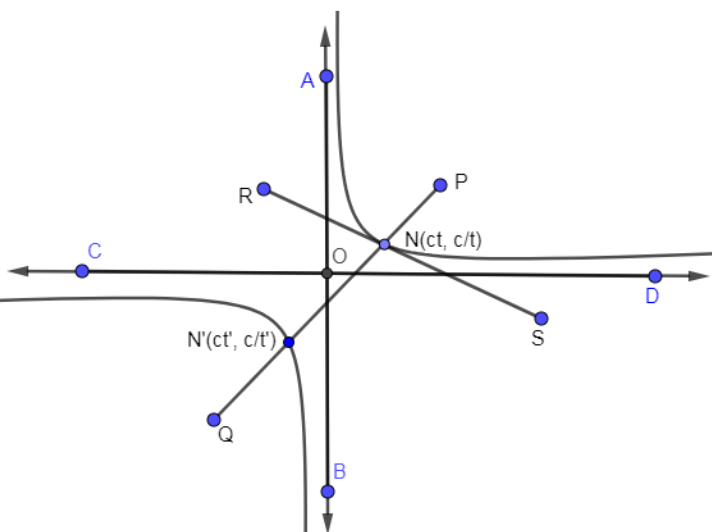
In the above diagram, RS is tangent at point N $(ct,\dfrac{c}{t})$ and PQ is the normal at point N $(ct,\dfrac{c}{t})$ which meets the hyperbola again at N’ $(c{{t}^{'}},\dfrac{c}{{{t}^{'}}})$.
So, let's find the equation of normal, for that we first have to find the slope which is $\dfrac{-dx}{dy}$
So for that we will find $\dfrac{dy}{dx}$ by differentiating $xy={{c}^{2}}$ at point $(ct,\dfrac{c}{t})$
On differentiating we get $1y+x\dfrac{dy}{dx}=0$ which on solving gives
$\dfrac{dy}{dx}=\dfrac{-y}{x}$but we want value of$\dfrac{-dx}{dy}$, which is equal to
$\dfrac{-dx}{dy}=\dfrac{x}{y}$ , on putting value of point $(ct,\dfrac{c}{t})$
$\dfrac{-dx}{dy}=\dfrac{c{{t}^{2}}}{c}={{t}^{2}}$
So, we have the point $(ct,\dfrac{c}{t})$ passing through normal as well as slope of normal ${{t}^{2}}$
So, the equation of normal will be using property $y-{{y}_{1}}=(x-{{x}_{1}})m$
On putting $x=ct,y=\dfrac{c}{t},m={{t}^{2}}$ , we get equation of normal as
$y-\dfrac{c}{t}=(x-ct){{t}^{2}}$
But it's given that it passes through point $(c{{t}^{'}},\dfrac{c}{{{t}^{'}}})$ also
So, we will put this point in our equation
On putting $x=c{{t}^{'}},y=\dfrac{c}{{{t}^{'}}}$ in equation $y-\dfrac{c}{t}=(x-ct){{t}^{2}}$
We get $\dfrac{c}{{{t}^{'}}}-\dfrac{c}{t}=(c{{t}^{'}}-ct){{t}^{2}}$
On solving gives $\dfrac{1}{{{t}^{'}}}-\dfrac{1}{t}=({{t}^{'}}-t){{t}^{2}}$
Which on further solving gives $\dfrac{t-{{t}^{'}}}{t{{t}^{'}}}=({{t}^{'}}-t){{t}^{2}}$
Cancelling $({{t}^{'}}-t)$ we finally get ${{t}^{'}}=-\dfrac{1}{{{t}^{3}}}$
Hence answer is ${{t}^{'}}=-\dfrac{1}{{{t}^{3}}}$ option (A).

Note: Most of the students while in hurry take the slope of tangent and forgets to consider the slope of normal which results in the wrong answer. The equation of the tangent and normal at Point$(ct,\dfrac{c}{t})$ of rectangular hyperbola by = c2 are $x+y-{{t}^{2}}-2ct=0$and $x{{t}^{3}}-ty-c{{t}^{4}}+c=0$respectively ,remember it directly