Question
Question: If the normal at any point P on the ellipse \(\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = ...
If the normal at any point P on the ellipse a2x2+b2y2=1 meets the axes in G and g respectively, then the ratio PG:Pg is equal to
A. a:b
B. a2:b2
C. b:a
D. b2:a2
Solution
In this question, we need to determine the ratio of PG:Pg such that the normal at any point P on the ellipse a2x2+b2y2=1 meets the axes in G and g respectively. For this, we use the equation of the normal to the given ellipse.
First, we are going to find the coordinates of g and G and then we are going to find the distance from the point on the normal and then we are going to find the ratio for which is asked in the question and then simplify it to get the answer.
Formula Used: axsecθ−ybcosecθ=a2−b2
Complete step by step answer:
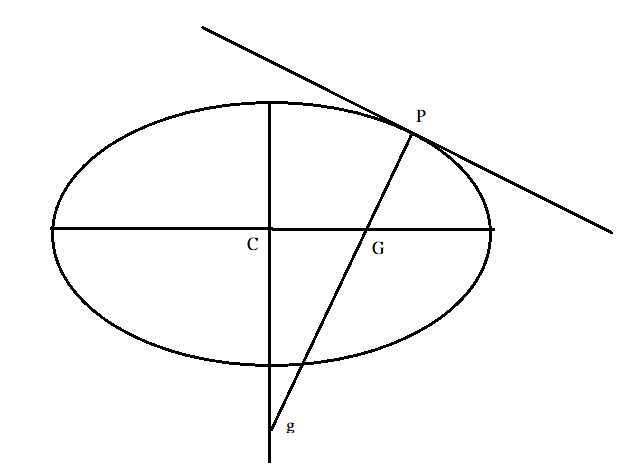
Let P≡(a cos θ , b sin θ)
The equation of the normal to the given ellipse at P is given by axsecθ−ybcosecθ=a2−b2
Therefore,
G≡((a−ab2)cosθ,0) and g≡(0,(b−ba2)sinθ)
Thus,
Also,
Pg=(a2cos2θ+b2a4sin2θ) =ba(b2cos2θ+a2sin2θ)Now, dividing PG and Pg values, we get
PgPG=ba(b2cos2θ+a2sin2θ)ab(b2cos2θ+a2sin2θ) =a2b2
Therefore, if the normal at any point P on the ellipse a2x2+b2y2=1 meets the axes in G and g respectively, then the ratio PG : Pg is equal to a2b2.
So, the correct answer is Option D.
Note: There might be confusion in the points of G and g. Normal is defined as the line passing through the point of contact which is perpendicular to the tangent.
An ellipse is defined as the plane curve surrounding two focal points such that for all the points on the curve, the sum of the two distances to the focal points is a constant.
The equation of the standard ellipse centered at the origin with the width 2a and the height 2b is given by
a2x2+b2y2=1
If the equation of the ellipse is
a2x2+b2y2=1
Then, the point form equation of the normal at point (x1,y1) is y−y1=x1b2y1a2(x−x1),x1=0
