Question
Question: If the midpoint of the segment AB is (1, 4), the coordinates of A are (2, – 3). How do you find the ...
If the midpoint of the segment AB is (1, 4), the coordinates of A are (2, – 3). How do you find the coordinate of point B?
Solution
We are given that the midpoint of segment AB is (1, 4) and we are given the coordinate of one endpoint and we are asked to find the other. To find this we will first learn how the points and the ratio in which the points divide the line segmented connected are. Then we will use the section formula X=m1+m2m1x2+m2x1 and Y=m1+m2m1y2+m2y1. We will use the coordinate of A and the midpoint to find the coordinate of B. We will also learn about a short trick to do such problems.
Complete step by step answer:
We are given that we have a line segment AB whose midpoint is (1, 4). The midpoint is the points that will divide the line into two equal ratios. If we consider that X is the midpoint of AB then AX = XB. So, the ratio of AX:XB will be
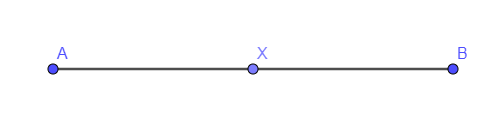
XBAX=AXAX[As XB=AX]
⇒XBAX=11
Therefore the ratio is 1:1.
Now, we will use the section formula. The section formula tells us about how the points cutting the line segment into sections are connected to the coordinate of the endpoint of the line segment. If we have

X divides it into ratio m1:m2 then the coordinate of X is given as
X=m1+m2m1x2+m2x1
Y=m1+m2m1y2+m2y1
In our problem we have coordinates of A as (2, – 3). So, (x1,y1)=(2,−3) and the coordinate of midpoint X as (1, 4). So, (x, y) = (1, 4). We have to find the value of coordinates of B, we have it as B(x2,y2). So as we have that ratio as 1:1, so m1=1 and m2=1. Now, we use these values in
X=m1+m2m1x2+m2x1
⇒1=1+11×x2+1(2)
On simplifying, we get,
⇒1=2x2+2
Solving for x2 we get,
⇒x2+2=2
⇒x2=0
Now, using the value on Y=m1+m2m1y2+m2y1 we get
⇒4=1+11×y2+(−3)
On simplifying, we get,
⇒4=2y2−3
Solving for y2 we get,
⇒8=y2−3
⇒y2=11
So, we get x2=0 and y2=11. So, the coordinate of B is (0, 11)
Note: We can also solve the problem in which are given the midpoint, as we have a midpoint formula given to us as x=2x1+x2 and y=2y1+y2. Now as x = 1 and x1=2, so we get,
⇒1=22+x2
On simplifying, we get,
⇒2=2+x2
Hence,
⇒x2=0
Now, we have y1=−3 and y = 4, so we get,
4=2−3+y2
On simplifying, we get,
8=−3+y2
Solving for y2 we get,
⇒y2=11
So, the coordinate of B is (x2,y2)=(0,11).
