Question

If the midpoint of the line segment joining the points P(6,b-2) and Q(-2,4) is (2,-3), then find the value of b.

Answer 1

To solve this question, firstly we will identify the value of mid point O(x,y), $P({{x}_{1}},{{y}_{1}})$ and $Q({{x}_{2}},{{y}_{2}})$ on comparing with the values of points given in question. After that, we will use the formula of midpoint and using that formula, we will calculate the value of b and then we will find the y – coordinate of point P(6,b-2).

Complete step-by-step answer:
Now, we know that if a point say R( x,y ) bisects the line segment formed by joining the points $P({{x}_{1}},{{y}_{1}})$ and $Q({{x}_{2}},{{y}_{2}})$into two equal parts, then coordinates of point R will be $R\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$.
Now, in question it is given that ( 2, -3 ) is the midpoint of the line segment joining the points P(6,b-2) and Q(-2,4), which means ( 2, -3 ) bisects the line PQ into two equal parts.
So, let point be O(x,y) which is mid point of line PQ.

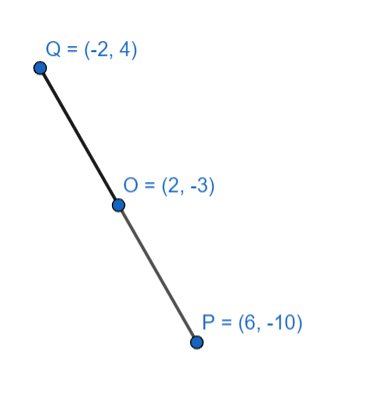
Here, it is given that coordinates of mid point are ( 2, -3 ).
So, x = 2 and y = - 3
Also, we discussed above that coordinates of point midpoints can be evaluated by$O\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$, where $P({{x}_{1}},{{y}_{1}})$ and $Q({{x}_{2}},{{y}_{2}})$.
So, we have
$2=\dfrac{6+(-2)}{2}$ and $-3=\dfrac{(b-2)+(4)}{2}$
Now, for y – coordinate we have
$-3=\dfrac{(b-2)+(4)}{2}$
On simplifying, we get
$-6=b+2$
On solving, we get
b = -8
so, coordinates of P will be P(6,-8-2)
or, P(6,-10)

Note: To solve such a type of question always remember that if we have a point which is the midpoint of a line segment, then it is also called the bisector of line. Also, remember that if a point say R( x,y ) bisects the line segment formed by joining the points $P({{x}_{1}},{{y}_{1}})$ and $Q({{x}_{2}},{{y}_{2}})$into two equal parts, then coordinates of point R will be $R\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$. Try not to make any calculation errors while solving the question.