Question

If the median AD of a triangle ABC divided the angle $\angle BAC$ in the ratio $1:2$, then $\dfrac{{\operatorname{Sin} B}}{{\operatorname{Sin} C}}$is equal to
A.$2\cos \dfrac{A}{3}$
B.$\dfrac{1}{2}\sec \dfrac{A}{3}$
C.$\dfrac{1}{2}\sin \dfrac{A}{3}$
D.$2\operatorname{cosec} \dfrac{A}{3}$

Answer 1

In order to find the value of $\dfrac{{\operatorname{Sin} B}}{{\operatorname{Sin} C}}$, first find the angles $\angle BAD$ and $\angle DAC$ using the ratio of $1:2$ in which $\angle BAC$ was divided. Then using the sine rule of the triangle, find the value of Sin B and Sin C, divide them, solve using the properties of trigonometry and get the results.
Formula used:
$\sin 2x = 2\sin x\cos x$
$\dfrac{1}{{\cos x}} = \sec x$

Complete answer:
Considering a triangle to be ABC, with median AD and sides as a, b and c. The diagram according to that is:

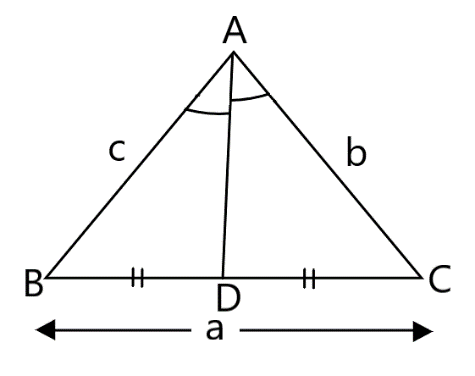
Since, $\angle BAC$ divides the angle A into ratio $1:2$. According to the ratio, let the angle be x and 2x.
So, the equation becomes:
$x + 2x = \angle A$
$\Rightarrow 3x = \angle A$
Dividing both sides by $3$:
$\Rightarrow \dfrac{{3x}}{3} = \dfrac{{\angle A}}{3}$
$\Rightarrow x = \dfrac{{\angle A}}{3}$
So, the angle becomes:
$\angle BAD = \dfrac{{\angle A}}{3}$
and
$\angle DAC = 2.\dfrac{{\angle A}}{3} = \dfrac{{2\angle A}}{3}$.
Now, the figure becomes:

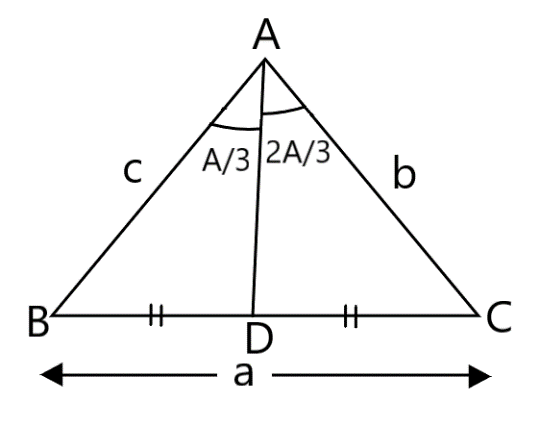
In Triangle ABD:
Using Sine Rule, we can write it as:
$\Rightarrow \dfrac{{AD}}{{BD}} = \dfrac{{\sin B}}{{\sin \dfrac{A}{3}}}$
Writing the above equation in form of Sin B, we get:
$\Rightarrow \sin B = \dfrac{{AD}}{{BD}}\sin \dfrac{A}{3}$ …….(1)
Now, In Triangle ACD:
Using Sine Rule, we can write it as:
$\Rightarrow \dfrac{{AD}}{{DC}} = \dfrac{{\sin C}}{{\sin \dfrac{{2A}}{3}}}$
Writing the above equation in form of Sin C, we get:
$\Rightarrow \sin C = \dfrac{{AD}}{{DC}}\sin \dfrac{{2A}}{3}$ …….(2)
Since, we need to find the value of $\dfrac{{\operatorname{Sin} B}}{{\operatorname{Sin} C}}$, so dividing the equation 1 by equation 2 and, we get:
$\Rightarrow \dfrac{{\sin B}}{{\sin C}} = \dfrac{{\dfrac{{AD}}{{BD}}\sin \dfrac{A}{3}}}{{\dfrac{{AD}}{{DC}}\sin \dfrac{{2A}}{3}}}$
Cancelling the common terms on the right side, we get:
$\Rightarrow \dfrac{{\sin B}}{{\sin C}} = \dfrac{{DC\sin \dfrac{A}{3}}}{{BD\sin \dfrac{{2A}}{3}}}$
Since, AD is the median and median divides the line BC into two, equal parts. So, $BD = DC$.
That gives:
$\Rightarrow \dfrac{{\sin B}}{{\sin C}} = \dfrac{{\sin \dfrac{A}{3}}}{{\sin \dfrac{{2A}}{3}}}$ ……(3)
From sub-angles, we know that:
$\sin 2x = 2\sin x\cos x$
So, we can write:
$\sin 2\dfrac{A}{3} = 2\sin \dfrac{A}{3}\cos \dfrac{A}{3}$
Substituting this equation in equation 3, we get:
$\Rightarrow \dfrac{{\sin B}}{{\sin C}} = \dfrac{{\sin \dfrac{A}{3}}}{{2\sin \dfrac{A}{3}\cos \dfrac{A}{3}}}$
Cancelling the common terms:
$\Rightarrow \dfrac{{\sin B}}{{\sin C}} = \dfrac{1}{{2\cos \dfrac{A}{3}}}$ ……(4)
Since, we know that $\dfrac{1}{{\cos x}} = \sec x$, so we can write $\dfrac{1}{{\cos \dfrac{A}{3}}} = \sec \dfrac{A}{3}$.
Substituting it in the above equation 4, we get:
$\Rightarrow \dfrac{{\sin B}}{{\sin C}} = \dfrac{1}{2}\sec \dfrac{A}{3}$.
Hence, the value of $\dfrac{{\operatorname{Sin} B}}{{\operatorname{Sin} C}}$is equal to $\dfrac{1}{2}\sec \dfrac{A}{3}$.
Therefore, Option B is correct.

Note:
The Sine Rule of a triangle basically represents the relation between the sides of the triangle and the angles of the triangle that is just opposite of the side (not-right angled).
It’s important to draw a figure of the triangle, in order to have a clear view of the sides and the angles.