Question
Question: If the mass m is in equilibrium, the magnitude of m is \(\left( g=10{ m }/{ { s }^{ 2 } } \right)\)....
If the mass m is in equilibrium, the magnitude of m is (g=10m/s2).
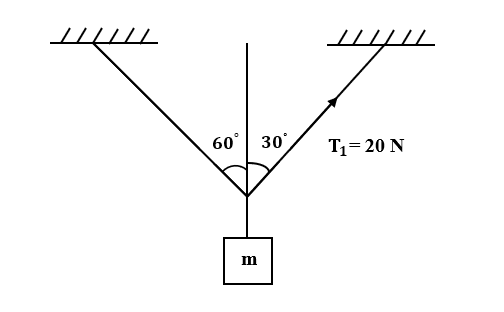
A.4kg
B.42kg
C.24kg
D.34kg
Solution
To solve this problem, first draw the free-body diagram and mention the forces along X and Y-axes. Then, equate the forces along the X-axis. Substitute the values and find the tension along another string i.e. T2. Then, use the balanced forces along the Y-axis. Substitute all the given and obtained values in this expression and find the value of m which is mass. This obtained value will be the magnitude of m.
Complete step-by-step answer:
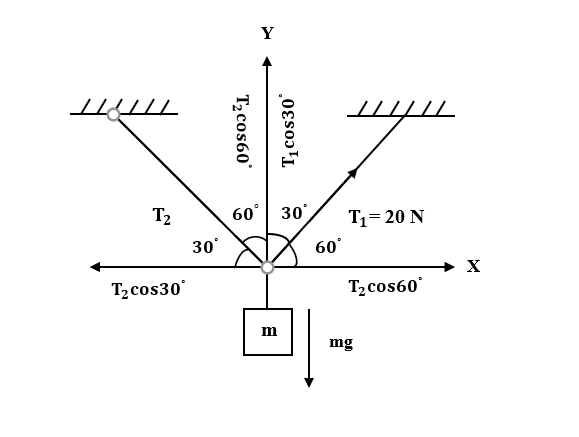
Given: T1=20N
g=10m/s2
In the figure drawn above, we can see on X-axis,
T1cos60°=T2cos30°
Substituting values in above equation we get,
20×21=T2×23
⇒20=T2×3
⇒T2=320
Along Y-axis,
T1cos30°+T2cos60°=mg
Substituting values in above equation we get,
20×23+320×21=m×10
⇒220(3+31)=m×10
⇒(3+31)=m
⇒m=34kg
Thus, the magnitude of m is 34kg.
So, the correct answer is option D i.e. 34kg.
So, the correct answer is “Option D”.
Note: To solve these types of questions, students must draw the free body diagram first. To draw a free body diagram, students must have a clear knowledge of free body diagrams. The diagrams used to represent forces and analyze them are called free body diagrams. These are pictorial representations of all the forces acting on the body due to contact with other objects or body objects acting on the body (such as gravity). These diagrams help us to understand the magnitude and direction of forces.
