Question
Question: If the lower spring is cut, find the acceleration of the blocks, immediately after cutting the sprin...
If the lower spring is cut, find the acceleration of the blocks, immediately after cutting the spring.
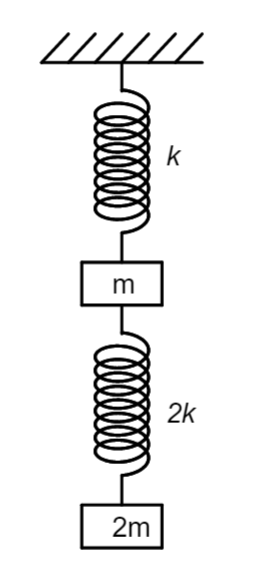
Solution
Use the free body diagram to denote all the forces acting on the blocks. A force acts on the block in a direction opposite to the elongation or stretch in the spring. Use Newton's second law to determine the value of acceleration for each block.
Formula used:
Fnet=ma
Complete answer:
A free body diagram is a labelled diagram which depicts every force acting on a body and is used to study a body in a system individually. It is used to alienate a body from a system and study its motion.
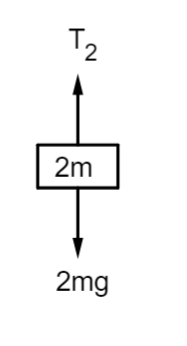
Now, studying the lower block individually. The free body diagram of the lower block can be seen as,
Here, T2 is the tension due to the lower spring constant 2k and g is acceleration due to gravity. The equation of motion at equilibrium can be written as,
T2=(2m)g
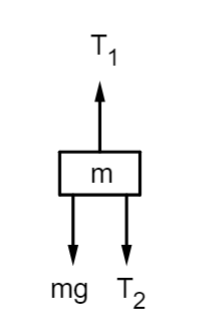
Now, let us look at the free body diagram of the upper block.
Here, T1 is tension due to the upper spring constant k. The equation of motion at equilibrium can be written as,
T1=T2+mg
Substitute the value of T2 as obtained above. Thus,
T1=2mg+mg=3mg
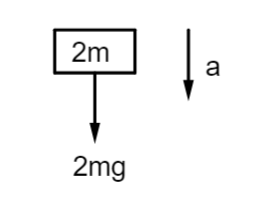
Now, just after the lower spring is cut, the lower mass falls below under the action of gravity and there is now no tension acting on the block due to spring. The free body diagram of lower block can now be seen as,
