Question
Question: If the locus of the complex number $z$ given by $arg(z+i)-arg(z-i)=\frac{2\pi}{3}$ is an arc of a ci...
If the locus of the complex number z given by arg(z+i)−arg(z−i)=32π is an arc of a circle, then the length of the arc is
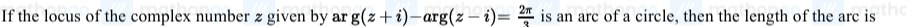
94π3
Solution
The given equation is arg(z+i)−arg(z−i)=32π.
Using the property arg(z1)−arg(z2)=arg(z2z1), we can rewrite the equation as: arg(z−iz+i)=32π
Let P1 be the point representing the complex number i, and P2 be the point representing the complex number −i. Let Z be the point representing the complex number z. The term z−i represents the vector P1Z. The term z+i represents the vector P2Z. The expression arg(z−iz+i) represents the angle from the vector P1Z to the vector P2Z. This angle is ∠P1ZP2. So, ∠P1ZP2=32π.
The points P1 and P2 are fixed points in the complex plane: P1=(0,1) and P2=(0,−1). The locus of a point Z such that the angle ∠P1ZP2 is constant is an arc of a circle passing through P1 and P2.
Let R be the radius of this circle and C be its center. The chord connecting P1 and P2 has length d=∣i−(−i)∣=∣2i∣=2. The angle subtended by this chord at any point Z on the arc is θ=32π.
Since θ=32π=120∘, which is greater than 90∘, the locus is the minor arc of the circle. The angle subtended by the chord P1P2 at the center C of the circle, let's call it α, is related to θ by α=2(π−θ). So, α=2(π−32π)=2(3π)=32π.
Now we need to find the radius R of the circle. Consider the triangle △P1CP2. It is an isosceles triangle with CP1=CP2=R. The angle ∠P1CP2=α=32π. Let M be the midpoint of the chord P1P2. M=(0,0). The length MP1=21∣P1P2∣=21(2)=1. In the right-angled triangle △CMP1, we have ∠MCP1=2α=21×32π=3π. Using trigonometry: sin(∠MCP1)=CP1MP1 sin(3π)=R1 23=R1 R=32
The length of the arc is given by the formula L=Rα, where α is the central angle in radians corresponding to the arc. L=32×32π=334π To rationalize the denominator, multiply by 33: L=3334π3=94π3
