Question
Question: If the lines $y = 3x + 1$ and $2y = x + 3$ are equally inclined to the line $y = mx + 4$, then $m =$...
If the lines y=3x+1 and 2y=x+3 are equally inclined to the line y=mx+4, then m=
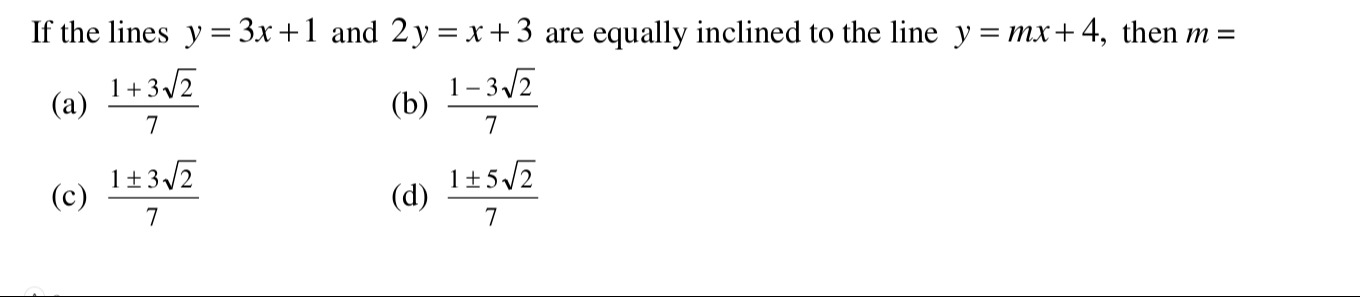
71+32
71−32
71±32
71±52
71±52
Solution
Let the slopes of the given lines y=3x+1, 2y=x+3, and y=mx+4 be m1, m2, and m3 respectively.
From the equations, we have: m1=3
2y=x+3⟹y=21x+23, so m2=21
m3=m
The condition that the lines y=3x+1 and 2y=x+3 are equally inclined to the line y=mx+4 means that the angle between the first line and the third line is equal to the angle between the second line and the third line.
Let θ1 be the angle between the line with slope m1 and the line with slope m3. Let θ2 be the angle between the line with slope m2 and the line with slope m3.
The angle θ between two lines with slopes ma and mb is given by tanθ=1+mambma−mb.
According to the problem, θ1=θ2, which implies tanθ1=tanθ2.
1+m1m3m1−m3=1+m2m3m2−m3
Substitute the values of m1 and m2:
1+3m3−m=1+21m21−m
1+3m3−m=22+m21−2m=2+m1−2m
This equation gives two possibilities:
Case 1: 1+3m3−m=2+m1−2m
(3−m)(2+m)=(1−2m)(1+3m)
6+3m−2m−m2=1+3m−2m−6m2
6+m−m2=1+m−6m2
6−m2=1−6m2
5m2=−5
m2=−1
This equation has no real solution for m.
Case 2: 1+3m3−m=−(2+m1−2m)=2+m2m−1
(3−m)(2+m)=(2m−1)(1+3m)
6+3m−2m−m2=2m+6m2−1−3m
6+m−m2=−m+6m2−1
Rearrange the terms to form a quadratic equation:
6m2+m2−m−m−1−6=0
7m2−2m−7=0
We solve this quadratic equation for m using the quadratic formula m=2a−b±b2−4ac.
Here, a=7, b=−2, c=−7.
m=2(7)−(−2)±(−2)2−4(7)(−7)
m=142±4+196
m=142±200
m=142±100×2
m=142±102
Factor out 2 from the numerator:
m=142(1±52)
m=71±52
The possible values of m are 71+52 and 71−52.
