Question

If the linear density of the rod of length L starting from one end (x=0) varies as $\text{ }\\!\\!\lambda\\!\\!\text{ }=\text{A}+\text{bx}$, then the center of mass of the rod will be at,
A) ${{X}_{C.M}}=\dfrac{L\left( 2A+bL \right)}{3\left( 3A+2bL \right)}$
B) ${{X}_{C.M}}=\dfrac{L\left( 3A+2bL \right)}{3\left( 2A+bL \right)}$
C) ${{X}_{C.M}}=\dfrac{L\left( 3A+2bL \right)}{3}$
D) ${{X}_{C.M}}=\dfrac{L\left( 2A+3bL \right)}{3}$

Answer 1

Hint: The center of a solid body can be calculated by taking a suitable cross section in the body, applying it in the center of mass formula for continuous bodies and integrating it throughout to get the center of mass.

Complete step by step answer:
In the problem we are given a rod of length L whose linear density varies as $\text{ }\\!\\!\lambda\\!\\!\text{ }=\text{A}+\text{bx}$. So in order to calculate the center of mass of the rod we need to take a small length dx on the rod at a distance x from x=0 and apply it in the center of mass formula and integrate from 0 to L to get the center of mass of the whole rod.

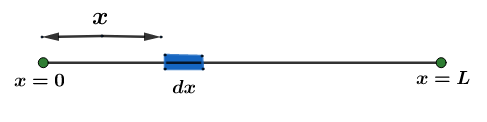
So the center of mass of a continuous body is given by,
$\text{C}\text{.M}=\dfrac{1}{\text{M}}\int{\text{xdm}}$
Here dm is the elemental mass of the small element dx that we had taken, its value can be written as, $dm=\lambda dx$
So substituting for dm, from the above equation we get,
$\text{C}\text{.M}=\dfrac{1}{M}\int{x(\lambda dx)}$
The limits of integration are from 0 to L.
$\text{C}\text{.M}=\dfrac{1 }{M}\int_{0}^{L}{(A+bx)xdx}$
Integrating and applying the limits, we get,
$C.M=\dfrac{(3A{{L}^{2}}+2b{{L}^{3}})}{6M}$
The total mass of the body M can be written as
$M=\int{\lambda dx=\int{(A+bx)dx}}$
$M=\int\limits_{0}^{L}{(A+bx)dx}=AL+\dfrac{b{{L}^{2}}}{2}$.
Substituting the value of total mass in the center of mass equation, we get
$C.M=\dfrac{(3A{{L}^{2}}+2b{{L}^{3}})}{3(2AL+b{{L}^{2}})}$
$\therefore \text{ C}\text{.M}=\dfrac{(3AL+2b{{L}^{2}})}{3(2A+bL)}$

So the answer to the question is option (B)- ${{X}_{C.M}}=\dfrac{L\left( 3A+2bL \right)}{3\left( 2A+bL \right)}$

Note:
The center of mass of a distribution of mass in space (sometimes referred to as the balance point) is the unique point where the weighted relative position of the distributed mass sums to zero. This is the point to which a force may be applied to cause a linear acceleration without an angular acceleration.