Question

If the line $y-\sqrt{3}x+3=0$ cuts the parabola ${{y}^{2}}=x+2$ at $A$ and $B$, then
$PA.PB$
is equal to [where $P=\left( \sqrt{3},0 \right)$]
(a) $\dfrac{4\left( \sqrt{3}+2 \right)}{3}$
(b) $\dfrac{4\left( 2-\sqrt{3} \right)}{3}$
(c) $\dfrac{4\sqrt{3}}{2}$
(d) $\dfrac{2\left( \sqrt{3}+2 \right)}{3}$

Answer 1

Hint: The parametric form of the equation of straight line, $\dfrac{x-{{x}_{1}}}{\cos \theta }=\dfrac{y-{{y}_{1}}}{\sin \theta }=r$ is used in this question.

Complete step-by-step answer:
The line given in the question is $y-\sqrt{3}x+3=0$ and the equation of the parabola is given as ${{y}^{2}}=x+2$.
It is said in the question that the line cuts the parabola at points $A$ and $B$. A point $P$ with coordinates $\left( \sqrt{3},0 \right)$ is also given. So, we can plot the graph with all the details as shown below,

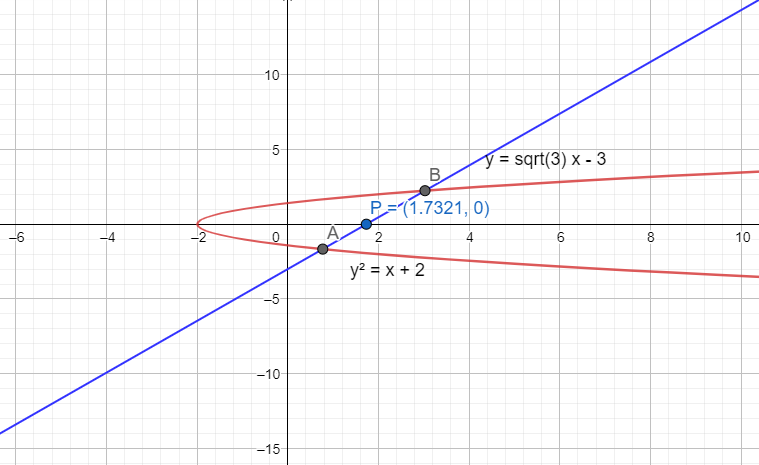
We need to find the values of $PA$ and $PB$ to solve the question. $PA$ and $PB$ represent the distance of the line joined by the points $P,A$ and $P,B$ respectively.
The parametric form of a straight line passing through the point $\left( {{x}_{1}},{{y}_{1}} \right)$ and making an angle of $\theta$ with the positive direction of the x-axis is given by,
$\dfrac{x-{{x}_{1}}}{\cos \theta }=\dfrac{y-{{y}_{1}}}{\sin \theta }=r\ldots \ldots \ldots (i)$
where $r$ is the distance between the two points with coordinates $\left( x,y \right)$ and $\left( {{x}_{1}},{{y}_{1}} \right)$.
In this question, $PA$ and $PB$ are equivalent to the distance $r$ mentioned above.
We have the coordinates of the point $\left( {{x}_{1}},{{y}_{1}} \right)=\left( \sqrt{3},0 \right)$. So, the first step is to find the angle $\theta$.
For that, we need to consider the equation of the line and rearrange it in the slope-intercept form,
$y-\sqrt{3}x+3=0$
$y=\sqrt{3}x-3$
Comparing it with the slope-intercept form given by $y=mx+c$, we get the slope as $m=\sqrt{3}=\tan \theta$.
The angle $\theta$ can hence be computed as below,

& \tan \theta =\sqrt{3} \\\ & \theta ={{\tan }^{-1}}\sqrt{3} \\\ & \theta =60{}^\circ \\\ \end{aligned}$$ Now substituting the obtained results in the equation $$(i)$$, $$\dfrac{x-\sqrt{3}}{\cos 60{}^\circ }=\dfrac{y-0}{\sin 60{}^\circ }=r$$ Substituting the values of $$\cos 60{}^\circ =\dfrac{1}{2},\sin 60{}^\circ =\dfrac{\sqrt{3}}{2}$$, we get, $$\dfrac{x-\sqrt{3}}{\dfrac{1}{2}}=\dfrac{y-0}{\dfrac{\sqrt{3}}{2}}=r$$ Equating both $$x$$ and $$y$$ to $r$, $$\dfrac{x-\sqrt{3}}{\dfrac{1}{2}}=r,\dfrac{y-0}{\dfrac{\sqrt{3}}{2}}=r$$ $$\begin{aligned} & x-\sqrt{3}=\dfrac{r}{2},y=\dfrac{\sqrt{3}}{2}r \\\ & x=\sqrt{3}+\dfrac{r}{2},y=\dfrac{\sqrt{3}}{2}r \\\ \end{aligned}$$ So, we have the coordinates of the point, $$A$$ or $$B$$ as $$\left( \sqrt{3}+\dfrac{r}{2},\dfrac{\sqrt{3}}{2}r \right)$$. As per the question, we know that this point cuts the parabola $${{y}^{2}}=x+2$$, so it can be substituted in the equation for the parabola as, $$\begin{aligned} & {{\left( \dfrac{\sqrt{3}}{2}r \right)}^{2}}=\left( \sqrt{3}+\dfrac{r}{2} \right)+2 \\\ & \dfrac{3{{r}^{2}}}{4}=\dfrac{r}{2}+\left( \sqrt{3}+2 \right) \\\ & \dfrac{3{{r}^{2}}}{4}-\dfrac{r}{2}-\left( \sqrt{3}+2 \right)=0 \\\ \end{aligned}$$ This is in the form of a quadratic equation in $r$, so we can get the values of $r$ using the formula as, $$\begin{aligned} & r=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a} \\\ & r=\dfrac{-\left( -\dfrac{1}{2} \right)\pm \sqrt{{{\left( -\dfrac{1}{2} \right)}^{2}}-4\times \left( \dfrac{3}{4} \right)\times -\left( \sqrt{3}+2 \right)}}{2\left( \dfrac{3}{4} \right)} \\\ & r=\dfrac{\dfrac{1}{2}\pm \sqrt{\dfrac{1}{4}+\left( \dfrac{12}{4} \right)\left( \sqrt{3}+2 \right)}}{\left( \dfrac{3}{2} \right)} \\\ \end{aligned}$$ Taking $\dfrac{1}{4}$ outside from the root, $$\begin{aligned} & r=\dfrac{\dfrac{1}{2}\pm \sqrt{\dfrac{1}{4}\left( 1+12\left( \sqrt{3}+2 \right) \right)}}{\left( \dfrac{3}{2} \right)} \\\ & r=\dfrac{\dfrac{1}{2}\pm \dfrac{1}{2}\sqrt{1+12\left( \sqrt{3}+2 \right)}}{\left( \dfrac{3}{2} \right)} \\\ \end{aligned}$$ Cancelling out $\dfrac{1}{2}$, $$r=\dfrac{1\pm \sqrt{1+12\left( \sqrt{3}+2 \right)}}{3}$$ Therefore, we have the roots as, $$\begin{aligned} & PA=\dfrac{1+\sqrt{1+12\left( \sqrt{3}+2 \right)}}{3} \\\ & PB=\dfrac{1-\sqrt{1+12\left( \sqrt{3}+2 \right)}}{3} \\\ \end{aligned}$$ Now, we can compute $$PA.PB$$ as, $$PA.PB=\dfrac{1+\sqrt{1+12\left( \sqrt{3}+2 \right)}}{3}\times \dfrac{1-\sqrt{1+12\left( \sqrt{3}+2 \right)}}{3}$$ Applying the identity $$\left( x+y \right)\left( x-y \right)={{x}^{2}}-{{y}^{2}}$$, $$\begin{aligned} & PA.PB=\dfrac{1}{9}\times \left[ {{1}^{2}}-{{\sqrt{1+12\left( \sqrt{3}+2 \right)}}^{2}} \right] \\\ & PA.PB=\dfrac{1}{9}\times \left[ 1-1-12\left( \sqrt{3}+2 \right) \right] \\\ & PA.PB=\dfrac{1}{9}\times \left[ -12\left( \sqrt{3}+2 \right) \right] \\\ & PA.PB=\dfrac{-12}{9}\times \left( \sqrt{3}+2 \right) \\\ & PA.PB=\dfrac{-4}{3}\times \left( \sqrt{3}+2 \right) \\\ \end{aligned}$$ We have to consider the modulus for the distance, so we get the value of $$PA.PB$$ as $$\left| \dfrac{-4\left( \sqrt{3}+2 \right)}{3} \right|=\dfrac{4\left( \sqrt{3}+2 \right)}{3}$$. Hence option (a) is the correct answer. Note: The last portion of the solution can be done more easily by using the fact that the product of the roots of a quadratic equation $$a{{x}^{2}}+bx+c=0$$ can be obtained as $$\dfrac{c}{a}$$. So, for this question,$\dfrac{3{{r}^{2}}}{4}-\dfrac{r}{2}-\left( \sqrt{3}+2 \right)=0$, the product of the roots $$PA$$ and $$PB$$ can be obtained as $$\begin{aligned} & PA.PB=\dfrac{-\left( \sqrt{3}+2 \right)}{\dfrac{3}{4}} \\\ & PA.PB=\dfrac{-4\left( \sqrt{3}+2 \right)}{3} \\\ & PA.PB=\left| \dfrac{-4\left( \sqrt{3}+2 \right)}{3} \right|\Rightarrow \dfrac{4\left( \sqrt{3}+2 \right)}{3} \\\ \end{aligned}$$