Question

If the line y = mx bisects the area enclosed by the lines x = 0, y = 0 x = $\frac{3}{2}$ and the curve y = 1 + 4x – x². Then the value of m is equal to-

• A. $\frac{13}{6}$
• B. $\frac{15}{6}$
• C. $\frac{13}{2}$
• D. $\frac{14}{4}$

Answer 1

Answer: (A)

$\frac{13}{6}$

Answer 2

We have, y = 1 + 4x – x²

Ž x² – 4x = –y + 1

Ž (x – 2)² = – (y – 5)

This equation represents a parabola having vertex at (2, 5) and opens downward. The area enclosed by this parabola and the line x = 0, y = 0, x = $\frac { 3 } { 2 }$ is shaded figure.

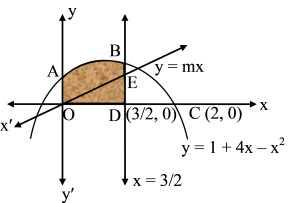
Since y = mx bisects the area of the shaded region. Therefore,

Area of the region ODBAO = 2 Area of the region ODEO

Ž $\int _ { 0 } ^ { 3 / 2 }$ (1 + 4x – x²) dx = 2 $\int _ { 0 } ^ { 3 / 2 } \mathrm { mx }$ dx

Ž $\left[ x + 2 x ^ { 2 } - \frac { x ^ { 3 } } { 3 } \right] _ { 0 } ^ { 3 / 2 }$ = 2m $\left[ \frac { x ^ { 2 } } { 2 } \right] _ { 0 } ^ { 3 / 2 }$

Ž $\frac { 3 } { 2 }$ + – $\frac { 9 } { 8 }$ = m × $\frac { 9 } { 4 }$ Ž $\frac { 39 } { 8 }$ = Ž m =$\frac { 13 } { 6 }$.

Hence (1) is the correct answer.