Question

If the line $x-y=-4K$ is a tangent to the parabola ${{y}^{2}}=8x$ at point P, then the perpendicular distance of normal at P from $\left( K,2K \right)$ is?
(a) $\dfrac{5}{2\sqrt{2}}$
(b) $\dfrac{7}{2\sqrt{2}}$
(c) $\dfrac{9}{\sqrt{5}}$
(d) $\dfrac{1}{2\sqrt{2}}$

Answer 1

We start solving the problem by comparing the given equation of the parabola with the standard equation. We then compare the given equation with the standard slope form of the equation of the tangent of parabola which leads us to finding the point P and the value of K. We then find the equation of the normal by using the fact that they are perpendicular to each other. We then find the point $\left( K,2K \right)$ and then find the perpendicular distance by using the fact that the perpendicular distance from the point $\left( {{x}_{1}},{{y}_{1}} \right)$ to the line $px+qy+r=0$ is $\dfrac{\left| p{{x}_{1}}+q{{y}_{1}}+r \right|}{\sqrt{{{p}^{2}}+{{q}^{2}}}}$.

Complete step by step answer:
According to the problem, we are given that the line $x-y=-4K$ is a tangent to the parabola ${{y}^{2}}=8x$ at point P. We need to find the perpendicular distance of normal at P from $\left( K,2K \right)$.

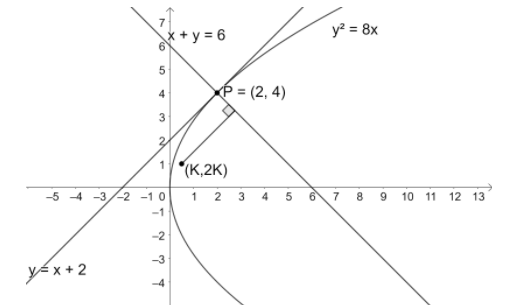
We know that the standard form of the parabola is ${{y}^{2}}=4ax$. Let us compare the given equation of parabola with the standard form.
We get $4a=8\Leftrightarrow a=2$ ---(1).
Let us rewrite the given equation of tangent in the form of $y=mx+c$. So, we get the equation of the tangent of parabola ${{y}^{2}}=8x$ as $y=x+4K$ ---(2).
We know that the slope form of the equation of the tangent of parabola ${{y}^{2}}=4ax$ is $y=mx+am$. Comparing this equation (2), we get $m=1$.
Also, $4K=2\times 1$.
$\Rightarrow 4K=2$.
$\Rightarrow K=\dfrac{1}{2}$ ----(3).
So, the equation of the tangent is $y=x+4\left( \dfrac{1}{2} \right)\Leftrightarrow y=x+2$. Let us find the point P by substituting this equation of y in ${{y}^{2}}=8x$.
So, we get ${{\left( x+2 \right)}^{2}}=8x$.
$\Rightarrow {{x}^{2}}+4x+4=8x$.
$\Rightarrow {{x}^{2}}-4x+4=0$.
$\Rightarrow {{\left( x-2 \right)}^{2}}=0$.
$\Rightarrow x-2=0$.
$\Rightarrow x=2$.
Now, let find the y coordinate of the point P.
So, we get $y=2+2=4$.
So, the point P is $\left( 2,4 \right)$.
We know that the product of slopes of tangent and normal of any conic is $-1$ as they are perpendicular to each other. Let us assume the slope of the normal be ${{m}_{1}}$.
So, we get $1\times {{m}_{1}}=-1\Leftrightarrow {{m}_{1}}=-1$. This tells that the normal passes through the point $P\left( 2,4 \right)$ having slope –1.
We know that the equation of the slope passing through the point $\left( {{x}_{1}},{{y}_{1}} \right)$ and having slope m is $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$.
The equation of the normal at point P is $y-4=-1\left( x-2 \right)$.
$\Rightarrow y-4=-x+2$.
$\Rightarrow x+y-6=0$ ---(4).
Now, let us find the point $\left( K,2K \right)$.
From equation (3), we get $\left( K,2K \right)=\left( \dfrac{1}{2},2\left( \dfrac{1}{2} \right) \right)=\left( \dfrac{1}{2},1 \right)$.
Now, we need to find the perpendicular distance from the point $\left( \dfrac{1}{2},1 \right)$ to the line $x+y-6=0$.
We know that the perpendicular distance from the point $\left( {{x}_{1}},{{y}_{1}} \right)$ to the line $px+qy+r=0$ is $\dfrac{\left| p{{x}_{1}}+q{{y}_{1}}+r \right|}{\sqrt{{{p}^{2}}+{{q}^{2}}}}$.
So, we get the perpendicular distance from the point $\left( \dfrac{1}{2},1 \right)$ to the line $x+y-6=0$ as $\dfrac{\left| \dfrac{1}{2}+1-6 \right|}{\sqrt{{{\left( \dfrac{1}{2} \right)}^{2}}+{{1}^{2}}}}$.
$\Rightarrow \dfrac{\left| \dfrac{1}{2}+1-6 \right|}{\sqrt{{{\left( \dfrac{1}{2} \right)}^{2}}+{{1}^{2}}}}=\dfrac{\left| \dfrac{1}{2}-5 \right|}{\sqrt{\dfrac{1}{4}+1}}$.
$\Rightarrow \dfrac{\left| \dfrac{1}{2}+1-6 \right|}{\sqrt{{{\left( \dfrac{1}{2} \right)}^{2}}+{{1}^{2}}}}=\dfrac{\left| \dfrac{-9}{2} \right|}{\sqrt{\dfrac{5}{4}}}$.
$\Rightarrow \dfrac{\left| \dfrac{1}{2}+1-6 \right|}{\sqrt{{{\left( \dfrac{1}{2} \right)}^{2}}+{{1}^{2}}}}=\dfrac{\dfrac{9}{2}}{\dfrac{\sqrt{5}}{2}}$.
$\Rightarrow \dfrac{\left| \dfrac{1}{2}+1-6 \right|}{\sqrt{{{\left( \dfrac{1}{2} \right)}^{2}}+{{1}^{2}}}}=\dfrac{9}{\sqrt{5}}$.
So, we have found the perpendicular distance as $\dfrac{9}{\sqrt{5}}$.

So, the correct answer is “Option c”.

Note: We can also find the equation of the tangent (value of K) by substituting the given equation in the equation of the parabola and using the fact that the obtained quadratic equation should have equal roots. We can see that the given problem contains a heavy amount of calculation, so we need to perform each step carefully. We should not forget to apply the modulus while calculating the perpendicular distance as the distance is always positive.