Question

If the line segment joining the points A (a, b) and B (c, d) subtends an angle $\theta$ at the origin, then $\cos \theta$ is equal to:
(a) $\dfrac{ac-bc}{\sqrt{\left( {{a}^{2}}+{{b}^{2}} \right)\left( {{c}^{2}}+{{d}^{2}} \right)}}$
(b) $\dfrac{ac+bd}{\sqrt{\left( {{a}^{2}}+{{b}^{2}} \right)\left( {{c}^{2}}+{{d}^{2}} \right)}}$
(c) $\dfrac{ac+cd}{\sqrt{\left( {{a}^{2}}+{{b}^{2}} \right)\left( {{c}^{2}}+{{d}^{2}} \right)}}$
(d) None of these

Answer 1

Hint: In this question, we will first visualize the given situation and then we will try to apply the trigonometric formula, that is $\cos \left( \alpha -\beta \right)=\cos \alpha \cos \beta +\sin \alpha \sin \beta$. Also, we should know that $\cos \alpha =\dfrac{\text{base}}{\text{hypotenuse}}$ and $\sin \alpha =\dfrac{\text{perpendicular}}{\text{hypotenuse}}$.

Complete step-by-step answer:
In this question, we have to find the value of $\cos \theta$ where $\theta$ is the angle subtended by the line joining A (a, b) and B (c, d) at the origin. Here, we can represent the given situation as,

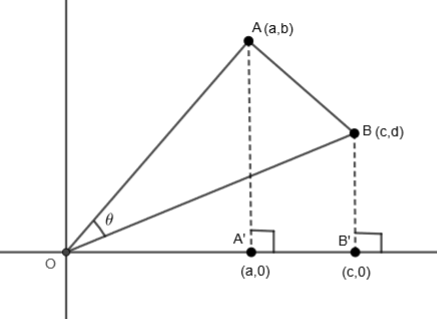
We have been given that the coordinates of A and B are (a, b) and (c, d) respectively. So, we can write the coordinates of A’ and B’ as (a, 0) and (c, 0) on the x and y axis. Let us consider $\angle AOA'$ as $\alpha$ and $\angle BOB'$ as $\beta$. So, we can write,
$\theta =\alpha -\beta ....\left( i \right)$
So, from the figure, we can say that
$\cos \alpha =\dfrac{OA'}{OA}$
$\cos \beta =\dfrac{OB'}{OB}$
By using the distance formula, that is $\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$, we will find the value of OA’, OA, OB’ and OB. So, we get,
$OA'=\sqrt{{{\left( a-0 \right)}^{2}}+{{\left( 0-0 \right)}^{2}}}=a$
$OB'=\sqrt{{{\left( c-0 \right)}^{2}}+{{\left( 0-0 \right)}^{2}}}=c$
$OA=\sqrt{{{\left( a-0 \right)}^{2}}+{{\left( b-0 \right)}^{2}}}=\sqrt{{{a}^{2}}+{{b}^{2}}}$
$OB=\sqrt{{{\left( c-0 \right)}^{2}}+{{\left( d-0 \right)}^{2}}}=\sqrt{{{c}^{2}}+{{d}^{2}}}$
$AA'=\sqrt{{{\left( a-a \right)}^{2}}+{{\left( b-0 \right)}^{2}}}=b$
$BB'=\sqrt{{{\left( c-c \right)}^{2}}+{{\left( d-0 \right)}^{2}}}=d$
So, we get,
$\cos \alpha =\dfrac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$
$\cos \beta =\dfrac{c}{\sqrt{{{c}^{2}}+{{d}^{2}}}}$
And, we know that
$\sin \alpha =\dfrac{AA'}{OA}$ and $\sin \beta =\dfrac{BB'}{OB}$
$\sin \alpha =\dfrac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$ and $\sin \beta =\dfrac{d}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$
And we know that $\theta =\alpha -\beta$. So, we will take cosine ratios to both sides.
$\cos \theta =\cos \left( \alpha -\beta \right)$
Now, we know that,
$\cos \left( \alpha -\beta \right)=\cos \alpha \cos \beta +\sin \alpha \sin \beta$
So, we get,
$\cos \theta =\cos \alpha \cos \beta +\sin \alpha \sin \beta$
Now, we will put the values of $\cos \alpha$, $\cos \beta$, $\sin \alpha$ and $\sin \beta$ in the above equation. So, we will get,
$\cos \theta =\dfrac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\times \dfrac{c}{\sqrt{{{c}^{2}}+{{d}^{2}}}}+\dfrac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\times \dfrac{d}{\sqrt{{{c}^{2}}+{{d}^{2}}}}$
$\cos \theta =\dfrac{ac+bd}{\sqrt{{{a}^{2}}+{{b}^{2}}}\sqrt{{{c}^{2}}+{{d}^{2}}}}$
Hence, option (b) is the right answer.

Note: In this question, it is necessary to visualize the condition by drawing the figure because visualization from the virtual figure won’t help. Also, we may make a mistake at the point where we found that $\theta =\alpha -\beta$. Also, considering the correct angles will only give the correct answer.