Question
Question: If the line passes through the points \[P\left( 6,-1,2 \right),Q\left( 8,-7,2\lambda \right)\] and \...
If the line passes through the points P(6,−1,2),Q(8,−7,2λ) and R(5,2,4) then value of λ is ___________.
(a) −3
(b) 0
(c) −1
(d) 2
Solution
Direction ratio of any line is calculated by any two points lying on it will be the same for a line.
Complete step-by-step answer:
As we have been given that the points P(6,−1,2),Q(8,−7,2λ) and R(5,2,4) are lying on a line
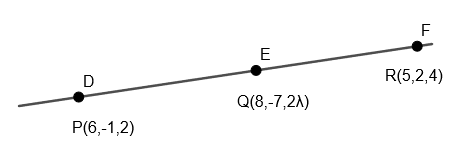
We know that as any line in 2D has slope like that, any line in 3D has direction ratio and direction cosine.
Now, the formula for direction ratio of any line if two points (x1,y1,z1) and (x2,y2,z2) are given.
dr=(x2−x1,y2−y1,z2−z1)
Let us calculate the direction ratio of the given line with the help of points P and R as following:
dr=(xR−xP,yR−yP,zR−zP)
dr=(5−6,2+1,4−2)
dr=(−1,3,2)....(i)
Let us calculate the direction ratio with the help of Q and R as follows.
dr=(xR−xQ,yR−yQ,zR−zQ)
dr=(−3,9,4−2λ).....(ii)
Since equation (i) and (ii) are representing the direction ratios of the same line, hence their ratios should be equal in the following way:
−3−1=93=4−2λ2
Taking the first two fractions from the above equation, we get that
31=93=31
Hence, it is verifying that the given line is linear if we see only the first two terms of the direction ratios. Now, in the third term of direction ratio, we have a variable λ which we need to find, and hence, the ratio 4−2λ2 should be equal to 31 as well.
31=4−2λ2
On cross – multiplying the above terms, we get
4−2λ=6
−2λ=2
λ=−1
Hence, we have λ=−1. To verify it, we can put λ=−1 in the equation (iii) as
31=31=4−2(−1)2=62=31
Hence, λ=−1 is the answer, i.e., option (c).
Note: We can solve the above question by calculating the ratio Q divides PQ
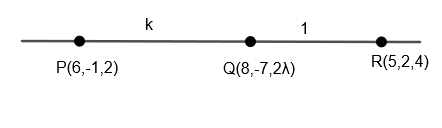
Let Q divide PR in (k:1) and we can write points Q by formulaM(m+nmx2+nx1,m+nmy2+ny1,m+nmz2+nz1) if two points A(x1,y1,z1) and B(x2,y2,z2) are given and point M can be written as above mentioned.
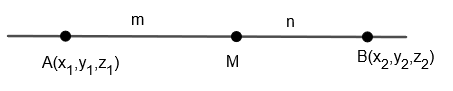
Hence, apply the above formula for calculating point Q.
⇒8=k+15k+6,−7=k+12k−1 and 2λ=k+14k+2
⇒5k+6=8k+8, −7k−7=2k−1 and 2λ=k+14k+2
3k=−2, −9k=6 and 2λ=k+14k+2
k=3−2,k=3−2
Hence, it is clear that points will lie on line as k=3−2 is calculated from the first two equations.
Now, 2λ=k+14k+2
2λk+2λ=4k+2
2λ×(3−2)+2λ=4×(3−2)+2
3−4λ+2λ=3−8+2
32λ=3−2⇒λ=−1
We have one more method where we can calculate the angle between two lines; here angle will be 180oif points lie on the line.
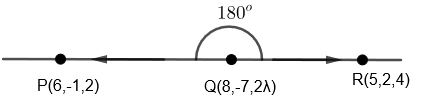
cos180o=∣QR∣.∣QP∣QR.QP=−1
QR=13i+9j+(4−2λ)k
QP=14i−8j+(2−2λ)k
By putting all these values in the equation (i), we can calculate ′λ′.
