Question
Question: If the line joining A(1, 3, 4) and B is divided by the point (-2, 3, 5) in the ratio 1:3, then B is:...
If the line joining A(1, 3, 4) and B is divided by the point (-2, 3, 5) in the ratio 1:3, then B is:
(a) (-11, 3, 8)
(b) (-11, 3, -8)
(c) (-8, 12, 20)
(d) (13, 6, -13)
Solution
Hint: In this question, we first need to draw the diagram with given conditions which gives a clear picture of what we have to find. Assume point B in terms of some variable and then solve for it using the two given points and the ratio by using the section formula.
Complete step-by-step answer:
(m1+m2m1x2+m2x1,m1+m2m1y2+m2y1)
Let us look at some of the basic definitions
COORDINATE GEOMETRY:
The branch of Mathematics in which geometrical problems are solved through algebra by using the coordinate system, is known as coordinate geometry.
RECTANGULAR AXIS:
Let XOX' and YOY' be two fixed straight lines, which meet at right angles at O. Then,
XOX' is called the axis of X or the X-axis or abscissa.
Y'OY is called axis of Y or the Y-axis or ordinate.
The ordered pair of real numbers (x, y) is called Cartesian coordinate.
Coordinates of the origin are (0, 0).
The X-coordinate of a point on Y-axis is zero.
Y-coordinate of a point on the X-axis is zero.
QUADRANTS: The X and Y-axis divide the coordinate plane into four parts, each part is called a quadrant.
DISTANCE FORMULA: Distance between two points (x1 , y1) and (x2 , y2) , is
(x2−x1)2+(y2−y1)2
Distance of the point (x1 , y1) from the origin is :
x12+y12
SECTION FORMULA:
The coordinate of the point which divides the joint of (x1 , y1) and (x2 , y2) in the ratio m1:m2
internally, is:
(m1+m2m1x2+m2x1,m1+m2m1y2+m2y1)
and externally is:
(m1−m2m1x2−m2x1,m1−m2m1y2−m2y1)
Now, let us assume the coordinates of B as (x, y, z).
The ratio as m:n such that,
m=1,n=3
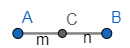
A=(1,3,4),C=(−2,3,5)
⇒C=(m+nmx2+nx1,m+nmy2+ny1,m+nmz2+nz1)
⇒C=(1+31⋅x+3⋅1,1+31⋅y+3⋅3,1+31⋅z+3⋅4)
⇒C=(4x+3,4y+9,4z+12)
Now, on equating this with the coordinates of C we get,
⇒(−2,3,5)=(4x+3,4y+9,4z+12)
Now, on equating each coordinate respectively we get,
