Solveeit Logo
Login

Question

Question: If the line \(\dfrac{x-3}{1}=\dfrac{y+2}{-1}=\dfrac{z+\lambda }{-2}\) lies on the plane \(2x-4y+3z=2...

If the line x−31=y+2−1=z+λ−2\dfrac{x-3}{1}=\dfrac{y+2}{-1}=\dfrac{z+\lambda }{-2} lies on the plane 2x−4y+3z=22x-4y+3z=2, then the shortest distance between this line and the line x−112=y9=z4\dfrac{x-1}{12}=\dfrac{y}{9}=\dfrac{z}{4} is:
(a) 0
(b) 2
(c) 1
(d) 3

Explanation

Solution

First of all, we have to find the value of λ\lambda in the equation of line x−31=y+2−1=z+λ−2\dfrac{x-3}{1}=\dfrac{y+2}{-1}=\dfrac{z+\lambda }{-2}. As it is given that this line x−31=y+2−1=z+λ−2\dfrac{x-3}{1}=\dfrac{y+2}{-1}=\dfrac{z+\lambda }{-2} lies on the plane 2x−4y+3z=22x-4y+3z=2 so the coordinates of the point lying on the line will satisfy this equation of plane. We can equate the equation of line x−31=y+2−1=z+λ−2\dfrac{x-3}{1}=\dfrac{y+2}{-1}=\dfrac{z+\lambda }{-2} to k so the equation of line will look like x−31=y+2−1=z+λ−2=k\dfrac{x-3}{1}=\dfrac{y+2}{-1}=\dfrac{z+\lambda }{-2}=k. Now, find the values of x, y, z in terms of k and λ\lambda then substitute these values of x, y and z in the equation of plane. From there, we will get the value of λ\lambda . Now, we can find the shortest distance between two given lines by using the formula for square of the shortest distance between the lines:x−x1l1=y−y1m1=z−z1n1;\dfrac{x-{{x}_{1}}}{{{l}_{1}}}=\dfrac{y-{{y}_{1}}}{{{m}_{1}}}=\dfrac{z-{{z}_{1}}}{{{n}_{1}}}; x−x2l2=y−y2m2=z−z2n2\dfrac{x-{{x}_{2}}}{{{l}_{2}}}=\dfrac{y-{{y}_{2}}}{{{m}_{2}}}=\dfrac{z-{{z}_{2}}}{{{n}_{2}}} is equal to ∣x1−x2y1−y2z1−z2 l1m1n1 l2m2n2 ∣\left| \begin{matrix} {{x}_{1}}-{{x}_{2}} & {{y}_{1}}-{{y}_{2}} & {{z}_{1}}-{{z}_{2}} \\\ {{l}_{1}} & {{m}_{1}} & {{n}_{1}} \\\ {{l}_{2}} & {{m}_{2}} & {{n}_{2}} \\\ \end{matrix} \right| . And taking the square root of this determinant is the answer.

Complete step-by-step solution
We have given the equation of a line x−31=y+2−1=z+λ−2\dfrac{x-3}{1}=\dfrac{y+2}{-1}=\dfrac{z+\lambda }{-2} and also given that this line lies on the plane 2x−4y+3z=22x-4y+3z=2.
In the below diagram, we have drawn a plane 2x−4y+3z=22x-4y+3z=2 and also draw a line EF x−31=y+2−1=z+λ−2\dfrac{x-3}{1}=\dfrac{y+2}{-1}=\dfrac{z+\lambda }{-2} on the plane.

Now, let us find the value of λ\lambda by equating this equation of line by k.
x−31=y+2−1=z+λ−2=k\dfrac{x-3}{1}=\dfrac{y+2}{-1}=\dfrac{z+\lambda }{-2}=k
Now, we are going to calculate the coordinates of the point lie on this line as follows:
x−31=k ⇒x−3=k ⇒x=k+3 \begin{aligned} & \dfrac{x-3}{1}=k \\\ & \Rightarrow x-3=k \\\ & \Rightarrow x=k+3 \\\ \end{aligned}
y+2−1=k ⇒y+2=−k ⇒y=−k−2 \begin{aligned} & \dfrac{y+2}{-1}=k \\\ & \Rightarrow y+2=-k \\\ & \Rightarrow y=-k-2 \\\ \end{aligned}
z+λ−2=k ⇒z+λ=−2k ⇒z=−2k−λ \begin{aligned} & \dfrac{z+\lambda }{-2}=k \\\ & \Rightarrow z+\lambda =-2k \\\ & \Rightarrow z=-2k-\lambda \\\ \end{aligned}
From the above, we got the coordinates of point lying on the line as:
(k+3,−k−2,−2k−λ)\left( k+3,-k-2,-2k-\lambda \right)
Now, let us name the above point as P and which is passing through the line and also lying on the plane.

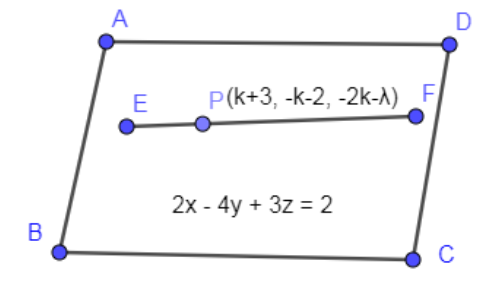
As the line is lying on the plane so point lying on the line also passes through the plane. Substituting (k+3,−k−2,−2k−λ)\left( k+3,-k-2,-2k-\lambda \right) in 2x−4y+3z=22x-4y+3z=2 we get,
2(k+3)−4(−k−2)+3(−2k−λ)=2 ⇒2k+6+4k+8−6k−3λ=2 ⇒0+14−3λ=2 ⇒14−2=3λ ⇒12=3λ ⇒λ=4 \begin{aligned} & 2\left( k+3 \right)-4\left( -k-2 \right)+3\left( -2k-\lambda \right)=2 \\\ & \Rightarrow 2k+6+4k+8-6k-3\lambda =2 \\\ & \Rightarrow 0+14-3\lambda =2 \\\ & \Rightarrow 14-2=3\lambda \\\ & \Rightarrow 12=3\lambda \\\ & \Rightarrow \lambda =4 \\\ \end{aligned}
Hence, we got the value of λ=4\lambda =4. Substituting this value of λ\lambda in equation of line x−31=y+2−1=z+λ−2\dfrac{x-3}{1}=\dfrac{y+2}{-1}=\dfrac{z+\lambda }{-2} we get,
x−31=y+2−1=z+4−2\dfrac{x-3}{1}=\dfrac{y+2}{-1}=\dfrac{z+4}{-2}
Now, we are going to find the shortest distance between the above line and x−112=y9=z4\dfrac{x-1}{12}=\dfrac{y}{9}=\dfrac{z}{4}.
We know, square of the shortest distance between two lines x−x1l1=y−y1m1=z−z1n1;\dfrac{x-{{x}_{1}}}{{{l}_{1}}}=\dfrac{y-{{y}_{1}}}{{{m}_{1}}}=\dfrac{z-{{z}_{1}}}{{{n}_{1}}}; x−x2l2=y−y2m2=z−z2n2\dfrac{x-{{x}_{2}}}{{{l}_{2}}}=\dfrac{y-{{y}_{2}}}{{{m}_{2}}}=\dfrac{z-{{z}_{2}}}{{{n}_{2}}} is equal to ∣x1−x2y1−y2z1−z2 l1m1n1 l2m2n2 ∣\left| \begin{matrix} {{x}_{1}}-{{x}_{2}} & {{y}_{1}}-{{y}_{2}} & {{z}_{1}}-{{z}_{2}} \\\ {{l}_{1}} & {{m}_{1}} & {{n}_{1}} \\\ {{l}_{2}} & {{m}_{2}} & {{n}_{2}} \\\ \end{matrix} \right|.
On comparing these two lines with the lines given in the above problem we get,
x−31=y−(−2)−1=z−(−4)−2\dfrac{x-3}{1}=\dfrac{y-\left( -2 \right)}{-1}=\dfrac{z-\left( -4 \right)}{-2}
x−112=y−09=z−04\dfrac{x-1}{12}=\dfrac{y-0}{9}=\dfrac{z-0}{4}
The values of x1,x2,y1,y2,z1,z2,l1,l2,m1,m2,n1,n2{{x}_{1}},{{x}_{2}},{{y}_{1}},{{y}_{2}},{{z}_{1}},{{z}_{2}},{{l}_{1}},{{l}_{2}},{{m}_{1}},{{m}_{2}},{{n}_{1}},{{n}_{2}} from the above lines are:
x1=3,x2=1; y1=−2,y2=0 z1=−4,z2=0 l1=1,l2=12 m1=−1,m2=9 n1=−2,n2=4 \begin{aligned} & {{x}_{1}}=3,{{x}_{2}}=1; \\\ & {{y}_{1}}=-2,{{y}_{2}}=0 \\\ & {{z}_{1}}=-4,{{z}_{2}}=0 \\\ & {{l}_{1}}=1,{{l}_{2}}=12 \\\ & {{m}_{1}}=-1,{{m}_{2}}=9 \\\ & {{n}_{1}}=-2,{{n}_{2}}=4 \\\ \end{aligned}
Substituting the above values in the above determinant we get,
∣3−1−2−0−4−0 1−1−2 1294 ∣ =∣2−2−4 1−1−2 1294 ∣ \begin{aligned} & \left| \begin{matrix} 3-1 & -2-0 & -4-0 \\\ 1 & -1 & -2 \\\ 12 & 9 & 4 \\\ \end{matrix} \right| \\\ & =\left| \begin{matrix} 2 & -2 & -4 \\\ 1 & -1 & -2 \\\ 12 & 9 & 4 \\\ \end{matrix} \right| \\\ \end{aligned}
If you can see the above determinant, you will find that first row is twice of second row and we know that whenever two rows are multiple of each other then the value of the determinant is 0.
So, square of the shortest distance between the given two lines is 0 so shortest distance between the two lines are 0.
Hence, the correct option is (a).

Note: In this problem, we have learned that if two lines in 3 - dimensions are given then how we can find the shortest distance between them. There is a point when you think that if we find the coordinates of the point lying on the line x−31=y+2−1=z+λ−2\dfrac{x-3}{1}=\dfrac{y+2}{-1}=\dfrac{z+\lambda }{-2} by equating this equation to k then we have two variables λ&k\lambda \And k so even when we put these coordinates in the equation of plane then we have one equation and two variables and how do we proceed and leave that problem there. Don’t do this mistake go on with this approach because after that you will find that the term “k” will be canceled out and you are just left with λ\lambda and then you can easily find the distance between two lines.