Question

If the line $2x+5y=12$ intersects the ellipse $4{{x}^{2}}+5{{y}^{2}}=20$ in two distinct points A and B, then find the midpoint of AB?
(a) $\left( 0,1 \right)$
(b) $\left( 1,2 \right)$
(c) $\left( 1,0 \right)$
(d) $\left( 2,1 \right)$

Answer 1

We start solving the problem by assuming the points A and B using which we find the midpoint of the AB. We then substitute the equation of the line in the equation of the ellipse to get quadratic equations in ‘x’ and ‘y’. We then use the fact that the sum of the roots of the quadratic equation $a{{x}^{2}}+bx+c=0$ is $\dfrac{-b}{a}$ to get the coordinates of the mid-points of AB.

Complete step-by-step solution:
According to the problem, we are given that the line $2x+5y=12$ intersects the ellipse $4{{x}^{2}}+5{{y}^{2}}=20$ in two distinct points A and B. We need to find the midpoint of AB.
Let us assume the point A and B be $A\left( {{x}_{1}},{{y}_{1}} \right)$ and $B\left( {{x}_{2}},{{y}_{2}} \right)$.
So, the midpoint of A and B is $\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$ ---(1).

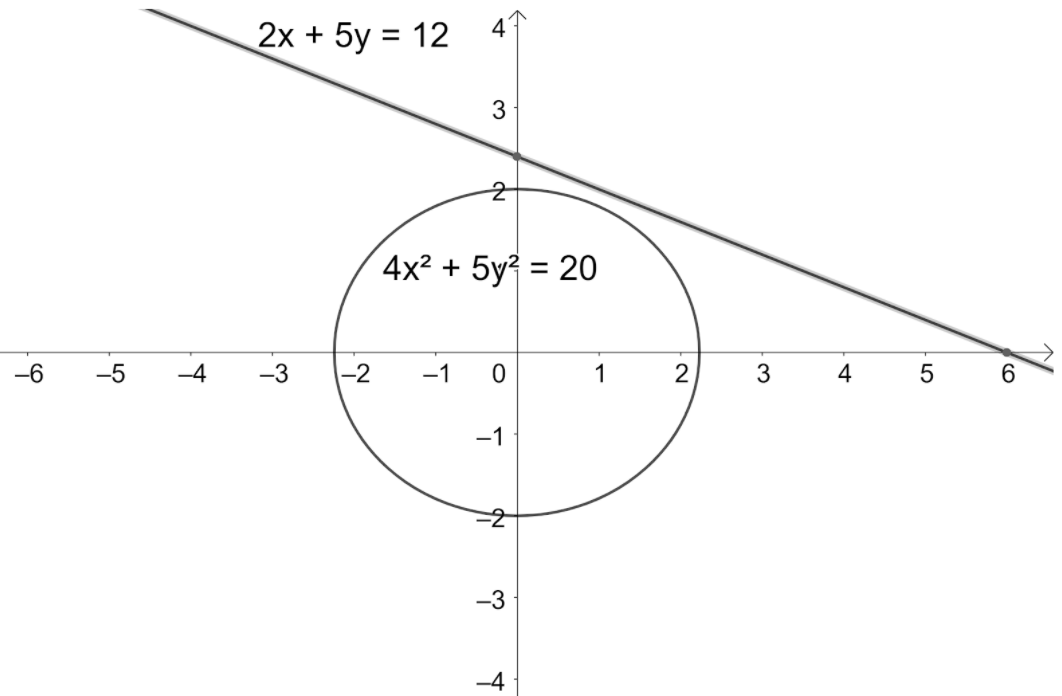
Now, we have the equation of the line $2x+5y=12$.
So, $2x=12-5y$.
$\Rightarrow x=6-\dfrac{5y}{2}$. Let us substitute this in $4{{x}^{2}}+5{{y}^{2}}=20$.
So, we get $4{{\left( 6-\dfrac{5y}{2} \right)}^{2}}+5{{y}^{2}}=20$.
$\Rightarrow 4\left( 36+\dfrac{25{{y}^{2}}}{4}-30y \right)+5{{y}^{2}}=20$.
$\Rightarrow 144+25{{y}^{2}}-120y+5{{y}^{2}}=20$.
$\Rightarrow 30{{y}^{2}}-120y+124=0$.
$\Rightarrow 15{{y}^{2}}-60y+62=0$.
The roots of this quadratic equation are the y-coordinates of the points of intersection of the line $2x+5y=12$ with the ellipse $4{{x}^{2}}+5{{y}^{2}}=20$.
This resembles the quadratic equation $a{{x}^{2}}+bx+c=0$, we know that the sum of the roots of this quadratic equation is $\dfrac{-b}{a}$.
So, we get ${{y}_{1}}+{{y}_{2}}=\dfrac{-\left( -60 \right)}{15}$.
$\Rightarrow {{y}_{1}}+{{y}_{2}}=\dfrac{60}{15}$.
$\Rightarrow {{y}_{1}}+{{y}_{2}}=4$.
$\Rightarrow \dfrac{{{y}_{1}}+{{y}_{2}}}{2}=2$ ---(2).
Now, we have the equation of the line $2x+5y=12$.
So, $5y=12-2x$.
$\Rightarrow y=\dfrac{12}{5}-\dfrac{2x}{5}$. Let us substitute this in $4{{x}^{2}}+5{{y}^{2}}=20$.
So, we get $4{{x}^{2}}+5{{\left( \dfrac{12}{5}-\dfrac{2x}{5} \right)}^{2}}=20$.
$\Rightarrow 4{{x}^{2}}+5\left( \dfrac{144}{25}+\dfrac{4{{x}^{2}}}{25}-\dfrac{48x}{25} \right)=20$.
$\Rightarrow 4{{x}^{2}}+\dfrac{144}{5}+\dfrac{4{{x}^{2}}}{5}-\dfrac{48x}{5}=20$.
$\Rightarrow \dfrac{24{{x}^{2}}}{5}+\dfrac{144}{5}-\dfrac{48x}{5}=20$.
$\Rightarrow 24{{x}^{2}}-48x+144=100$.
$\Rightarrow 24{{x}^{2}}-48x+44=0$.
$\Rightarrow 6{{x}^{2}}-12x+11=0$.
The roots of this quadratic equation are the x-coordinates of the points of intersection of the line $2x+5y=12$ with the ellipse $4{{x}^{2}}+5{{y}^{2}}=20$.
This resembles the quadratic equation $a{{x}^{2}}+bx+c=0$, we know that the sum of the roots of this quadratic equation is $\dfrac{-b}{a}$.
So, we get ${{x}_{1}}+{{x}_{2}}=\dfrac{-\left( -12 \right)}{6}$.
$\Rightarrow {{x}_{1}}+{{x}_{2}}=\dfrac{12}{6}$.
$\Rightarrow {{x}_{1}}+{{x}_{2}}=2$.
$\Rightarrow \dfrac{{{x}_{1}}+{{x}_{2}}}{2}=1$ ---(3).
Substituting equations (2) and (3) in equation (1), we get the midpoint of AB as $\left( 1,2 \right)$.
So, we have found the midpoint of AB as $\left( 1,2 \right)$.
The correct option for the given problem is (b).

Note: From the figure we can see that the line is not even touching the ellipse, which leads us to the points with coordinates as the complex numbers. We should know that the complex roots of the quadratic equation are distinct and the question didn’t mention that the points have to be real in this case. We can also solve this problem by substituting the options in the equation of the line to get the required option.