Question

If the letters of the word QUESTION are arranged at random, the probability that there will be exactly 2 letters in between Q and U is
a) $\dfrac{{}^{6}{{P}_{2}}}{8!}$
b) $\dfrac{{}^{6}{{P}_{2}}\times 2}{8!}$
c) $\dfrac{{}^{6}{{P}_{2}}\times 5!\times 2}{8!}$
d) $\dfrac{{}^{6}{{P}_{2}}\times 2}{8!}$

Answer 1

The word QUESTION has 8 letters. We need to arrange Q and U in such a way that there are only two letters in between them, i.e. \text{Q }\\!\\!\\_\\!\\!\text{ }\\!\\!\\_\\!\\!\text{ U}. So, we have to arrange 6 letters between them. Find different orientations in which the letters can be arranged. Also, find the number of orientations when Q and U are interchanged.

Complete step by step answer:
Now, use the given data to find the probability of exactly 2 letters in between Q and U.
Since total letters in word Question are 8. We have to arrange exactly two letters between Q and U. So, we need to choose 2 letters from the remaining 6 letters.
So, we have:${}^{6}{{C}_{2}}$
Next, as we can arrange the letters between Q and U in the following manner:

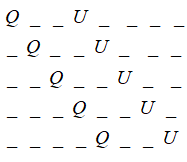
And similarly, by interchanging Q and U, we get:

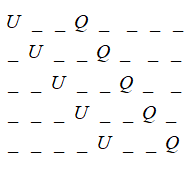
So, we can put the set of Q and U at 5 places, and could also arrange Q and U in 2 ways.
Therefore, the number of orientations is: $5!\times 2$
We need to choose exactly 2 letters between Q and U. So, the required probability is:
$=\dfrac{{}^{6}{{C}_{2}}\times 2!\times 4!}{8!}\times 5!\times 2$
Since, $C(n,r)=\dfrac{P(n,r)}{r!}$
We can write the probability as:
$=\dfrac{{}^{6}{{P}_{2}}}{8!}\times 5!\times 2$
So, the correct answer is “Option C”.

Note: While applying permutations and combinations, always be careful with the identities. Also, while finding the probability, always look for whichever orientation possible. Do not miss any orientation. And, do find the number of orientations when the letters are interchanged. Some might miss that case.