Question

If the length of three sides of a trapezium other than base is equal to 10 cm, then find the area of the trapezium when it is maximum.

Answer 1

Here, we are required to find the area of a trapezium when it is maximum. We are given three sides of the trapezium with which we would draw a trapezium and with the help of diagram, we would divide the trapezium in three parts and find the overall area of trapezium by adding all the three parts. To maximize the area, we would differentiate it and find the maximum possible value of one of the variables and hence, find the required answer.

Complete step-by-step answer:
To answer this question, first of all, we would draw a trapezium ABCD such that three of its sides (other than base) are 10 cm each.
Hence, AB$=$AD$=$CD$=$10 cm
Now, we would draw perpendiculars from A and D to the base BC such that,
AE and DF are the heights of the trapezium.

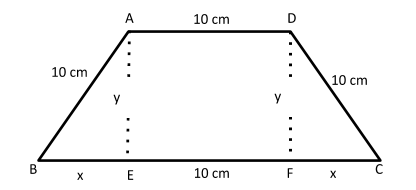
If we observe the above figure carefully, then AD is equal to EF,
Hence, EF$=$10 cm
Also, $\vartriangle AEB \cong \vartriangle DFC$
Because,
$\angle AEB = \angle DFC$ (AE and DF are perpendiculars, hence these angles are right angles)
AB$=$DC (Hypotenuse$=$10 cm ; given)
AE$=$DF (Height of the trapezium is same)
Hence, $\vartriangle AEB \cong \vartriangle DFC$ by RHS rule.
Therefore by CPCTC, i.e. corresponding parts of congruent triangles are equal.
Let BE$=$CF = $$$x$ cm Also, let the height of the trapezium = $AE$ = $DF$ = y$cm Now, area of $\vartriangle AEB = \dfrac{1}{2} \times $Base$ \times $Height $ = \dfrac{1}{2} \times $BE$ \times $AE $ = \dfrac{1}{2} \times x \times y$………………………………….(1) Similarly, area of $\vartriangle DFC = \dfrac{1}{2} \times $FC$ \times $DF $ = \dfrac{1}{2} \times x \times y$…………………………………(2) Now, area of the rectangle ADFE$$ = $$Length$ \times $Breadth $ = 10y$………………………………………...(3) Hence, area of trapezium$$ = $$Area of $\vartriangle AEB$ $ + $Area of $\vartriangle DFC$ $ + $Area of rectangle ADFE Hence, from(1),(2) and (3), Area of trapezium, A$$ = \dfrac{{xy}}{2} + \dfrac{{xy}}{2} + 10y$$ = \dfrac{{2xy}}{2} + 10y$$ = xy + 10y$Taking variable$y$common, A$ = y\left( {x + 10} \right)$…………………………….(4) Now, since$\vartriangle AEB$is a right angled triangle Therefore, by Pythagoras theorem,${\left( {AB} \right)^2} = {\left( {BE} \right)^2} + {\left( {AE} \right)^2}$$ \Rightarrow {\left( {10} \right)^2} = {\left( x \right)^2} + {\left( y \right)^2}$$ \Rightarrow {y^2} = 100 - {x^2}$Taking square root on both sides,$ \Rightarrow y = \sqrt {100 - {x^2}} $Substituting this value in equation (4) A$ = \sqrt {100 - {x^2}} \left( {x + 10} \right)$Now, we have to find the area of the trapezium when it is maximum. Hence, differentiating both sides with respect to$x$$ \Rightarrow \dfrac{{dA}}{{dx}} = \sqrt {100 - {x^2}} \left( 1 \right) + \left( {x + 10} \right)\dfrac{{ - 2x}}{{2\sqrt {100 - {x^2}} }}$This is because,$\left( {u.v} \right)' = u.\dfrac{{dv}}{{dx}} + v.\dfrac{{du}}{{dx}}$Solving further,$ \Rightarrow \dfrac{{dA}}{{dx}} = \sqrt {100 - {x^2}} - \dfrac{{x\left( {x + 10} \right)}}{{\sqrt {100 - {x^2}} }}$Now, taking LCM, we get,$ \Rightarrow \dfrac{{dA}}{{dx}} = \dfrac{{100 - {x^2} - x\left( {x + 10} \right)}}{{\sqrt {100 - {x^2}} }}$Now, put$\dfrac{{dA}}{{dx}} = 0$$ \Rightarrow \dfrac{{dA}}{{dx}} = \dfrac{{100 - {x^2} - x\left( {x + 10} \right)}}{{\sqrt {100 - {x^2}} }} = 0$Multiplying both sides by$\sqrt {100 - {x^2}} $$ \Rightarrow 100 - {x^2} - {x^2} - 10x = 0$$ \Rightarrow - 2{x^2} - 10x + 100 = 0$Taking$ - 2$common, we get,$ \Rightarrow - 2\left( {{x^2} + 5x - 50} \right) = 0$Dividing both sides by$ - 2$and doing middle term split$ \Rightarrow \left( {{x^2} + 10x - 5x - 50} \right) = 0$Now, taking common,$ \Rightarrow x\left( {x + 10} \right) - 5\left( {x + 10} \right) = 0$$ \Rightarrow \left( {x - 5} \right)\left( {x + 10} \right) = 0$Hence,$x - 5 = 0$$ \Rightarrow x = 5$Or$x + 10 = 0$$x = - 10$Clearly,$5 > - 10$Therefore, the maximum possible value of$x$is 5. Therefore, area of the trapezium when it is maximum is: A$ = \sqrt {100 - {x^2}} \left( {x + 10} \right)$Substitute$x = 5$$ \Rightarrow $A$ = \sqrt {100 - {{\left( 5 \right)}^2}} \left( {5 + 10} \right)$$ = \sqrt {100 - 25} .\left( {15} \right)$$ = \sqrt {75} .\left( {15} \right)$Prime factorization of 75 is: 75$ = $5$ \times $5$ \times $3 Hence,$\sqrt {75} = 5\sqrt 3 $Therefore, area of the trapezium when it is maximum is:$ = 15.5\sqrt 3 $$ = 75\sqrt 3 $$cm^2$
Hence, this is the required answer.

Note: To solve this question, we should know how to find the area of a trapezium and the two triangular parts inside the trapezium are congruent to each other. Also, we should know that in order to maximize the area, we are required to differentiate it and equate it to zero. Hence, there are various steps in this question where we could go wrong such as: while differentiating the area, while doing middle term split and specially while substituting the maximized value. Hence, complete attention is required while solving this question.