Question

If the length of the sides of the triangle are given as 3, 5 and 7 units. Find the largest angle of the triangle:
(a) ${{\cos }^{-1}}\left( \dfrac{13}{14} \right)$
(b) $\dfrac{2\pi }{3}$
(c) $\dfrac{3\pi }{3}$
(d) ${{\cos }^{-1}}\left( \dfrac{3}{4} \right)$

Answer 1

We use the fact that in a triangle, the largest angle lies opposite to the largest side of the triangle. We check the largest side of the triangle then apply cosine law to calculate the value of the largest angle. Since we have angles given in options in terms of $\pi$, we use the fact that value of $\pi ={{180}^{o}}$ and convert the obtained angle in terms of $\pi$.

Complete step-by-step answer :
Given that we have a triangle with length of the sides 3, 5 and 7 units. We need to find the largest angle of the triangle.
Let us assume the vertices of the triangle are A, B and C which are accordingly the angles of the triangle and let us assume the sides opposite to angles are $a=3$, $b=5$ and $c=7$ units. Here we assume that the side ‘a’ is opposite to the Angle ‘A’, side ‘b’ is opposite to the angle ‘B’ and side ‘c’ is opposite to the angle ‘C’.
Let us draw representing all the given information.

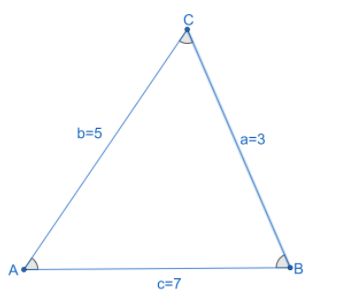
We know that the angle opposite to the largest side (largest in terms of length) is the largest angle for the triangle.
Here we have a greater side $c=7$ units. This makes ‘C’ as the largest angle of the triangle.
We use cosine rules to calculate angle ‘c’. We know that cosine rule for a triangle is defined as follows:
$\cos C=\dfrac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab}$.
We now substitute the values of a, b and c.
$\cos C=\dfrac{{{3}^{2}}+{{5}^{2}}-{{7}^{2}}}{2\times 3\times 5}$.
$\cos C=\dfrac{9+25-49}{30}$.
$\cos C=\dfrac{-15}{30}$.
$\cos C=\dfrac{-1}{2}$.
$C={{\cos }^{-1}}\left( \dfrac{-1}{2} \right)$.
$C={{120}^{o}}$.
We know that $\pi ={{180}^{o}}$.
$C={{120}^{o}}\times \dfrac{{{180}^{o}}}{{{180}^{o}}}$.
$C=\dfrac{2}{3}\times \pi$.
$C=\dfrac{2\pi }{3}$.
∴ The value of the largest angle of the triangle is $\dfrac{2\pi }{3}$.
The correct for the given problem is (b).

Note : Here we used cosine rule to calculate the angle as given angles are mostly in terms of cosine function. We can also calculate the angle by using sine rule. Here we can say that $\dfrac{2\pi }{3}$ will be the largest angle as the sum of the angles in a triangle is equal to ${{180}^{o}}$ or $\pi$.