Question

If the length of the perpendicular drawn from the origin to the line whose intercepts on the axes are a and b be p, then

1. ${a^2} + {b^2} = \dfrac{1}{{{p^2}}}$
2. ${a^2} + {b^2} = {p^2}$
3. $\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}} = \dfrac{2}{{{p^2}}}$
   4)$\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}} = \dfrac{1}{{{p^2}}}$

Answer 1

We can start by writing the equation of a line intercepts. It is given that the length of the perpendiculars are a, b and p. So, we can substitute these in the length of the perpendicular equation. By doing so, we can determine the relationship between a, b and p.
The basic formula used in the problem are:
$\dfrac{x}{a} + \dfrac{y}{b} = 1$
Where $a$is used to represent $x$intercept and $b$is to represent $y$intercept.
$d = \left| {\dfrac{c}{{\left( {{a^2} + {b^2}} \right)}}} \right|$

Complete step-by-step solution:

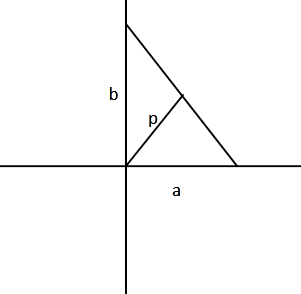
Let us consider the line in the form, $ax + by + c = 0$
The equation of a line in the intercept form is
$\dfrac{x}{a} + \dfrac{y}{b} = 1$
Rearranging this equation,
\eqalign{ & \Rightarrow \dfrac{x}{a} + \dfrac{y}{b} - 1 = 0 \cr & \Rightarrow bx + ay - ab = 0 \cr}
We know that the length of the perpendicular from the origin $\left( {0,0} \right)$to the given line $ax + by + c = 0$is given by, $d = \left| {\dfrac{c}{{\left( {{a^2} + {b^2}} \right)}}} \right|$
It is given that the perpendicular from origin to the given line is p.
$\Rightarrow p = \left| {\dfrac{{ab}}{{\sqrt {\left( {{b^2} + {a^2}} \right)} }}} \right|$
Squaring on both sides, we get,
\eqalign{ & \Rightarrow {p^2} = \dfrac{{{a^2}{b^2}}}{{\left( {{b^2} + {a^2}} \right)}} \cr & \Rightarrow \dfrac{1}{{{p^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}} \cr}
The final answer is $\dfrac{1}{{{p^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}$
Hence, the correct option is (4).
Additional Information:
On a graph, the point where the line crosses both the x-axis and the y-axis is called an intercept. The point of intersection of the line with the x-axis gives the x-intercept. The point of intersection of the line with the y-axis gives the y-intercept.

Note: The intercept equation and the perpendicular drawn to the line are two different equations. The equation for line and the equation for its intercept are similar, be careful while using them. Since the points are already given, substitute them for the known equations.