Question

If the length of the latus rectum of an ellipse is 4 units and the distance between a focus and its nearest vertex on the major axis is 3/2 units, then its eccentricity is?
${\text{A}}{\text{. }}\dfrac{1}{2}$
${\text{B}}{\text{. }}\dfrac{2}{3}$
${\text{C}}{\text{. }}\dfrac{1}{9}$
${\text{D}}{\text{. }}\dfrac{1}{3}$

Answer 1

Hint – We know the Focus = (ae, 0) and vertex = (a, 0) and the distance between focus and vertex = a(1-e) and eccentricity of the ellipse ${e^2} = 1 - \dfrac{{{b^2}}}{{{a^2}}}$. Use this to find the answer.

Complete step-by-step answer:
Now, according to the question,
Length of the latus rectum of an ellipse = 4 units.
Distance between a focus and its nearest vertex on the major axis is 3/2 units.
For better understanding refer the figure below-

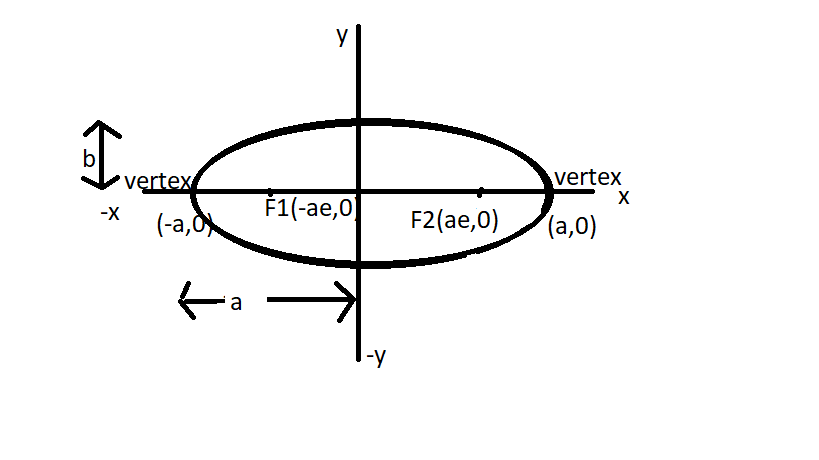
Now we know that the Focus = (ae, 0) and vertex = (a, 0) and the distance between focus and vertex = a(1-e).
Now,
$a(1 - e) = \dfrac{3}{2} \\\ \Rightarrow a - ae = \dfrac{3}{2} \\\ \Rightarrow a - \dfrac{3}{2} = ae \to (1) \\\$
Squaring the above equation, we get-
$\Rightarrow {a^2} + \dfrac{9}{4} - 3a = {a^2}{e^2} \to (2)$
Now, using the length of the latus rectum is given by $\dfrac{{2{b^2}}}{a}$.
We know the length of the latus rectum as given in the question is 4 units.
Therefore, $\dfrac{{2{b^2}}}{a} = 4 \\\ \Rightarrow {b^2} = 2a \to (3) \\\$
Now, we know eccentricity ${e^2} = 1 - \dfrac{{{b^2}}}{{{a^2}}} \\\ = 1 - \dfrac{{2a}}{{{a^2}}} \\\${from equation (3)}
$\Rightarrow {e^2} = 1 - \dfrac{2}{a} \to (4)$
Substituting this in equation (2), we get-
$\Rightarrow {a^2} + \dfrac{9}{4} - 3a = {a^2}\left( {1 - \dfrac{2}{a}} \right) \\\ \Rightarrow {a^2} + \dfrac{9}{4} - 3a = {a^2} - 2a \\\ \Rightarrow a = \dfrac{9}{4} \\\$
Therefore,
$\Rightarrow {e^2} = 1 - \dfrac{2}{a} \\\ \Rightarrow {e^2} = 1 - \dfrac{2}{{\dfrac{9}{4}}} \\\ \Rightarrow {e^2} = 1 - \dfrac{2}{9} \times 4 \\\ \Rightarrow {e^2} = 1 - \dfrac{8}{9} = \dfrac{1}{9} \\\ \Rightarrow e = \dfrac{1}{3} \\\$
Hence, the eccentricity of the given ellipse is $e = \dfrac{1}{3}$.

Note – Whenever such types of questions appear, then write the given things in the question and then by using the standard formula of the distance between focus and vertex = a(1-e) = 3/2. Squaring both the sides, we get, ${a^2} + \dfrac{9}{4} - 3a = {a^2}{e^2}$ and then using the standard formula of eccentricity of the ellipse ${e^2} = 1 - \dfrac{{{b^2}}}{{{a^2}}}$, find the value of e.