Question

If the length of subnormal is equal to the length of sub tangent at any point (3,4) on the curve y=f(x) and the tangent at (3,4) to y=f(x) meets the coordinate axis at A and B, the maximum area of $\vartriangle OAB.$ where O is origin, is

Answer 1

Important formulas used to solve such questions:
Length of subtangent- $y \times \dfrac{{dx}}{{dy}}$
Length of subnormal- $y \times \dfrac{{dy}}{{dx}}$
Equation of tangent passing through the point (a,b) and having slope m is given by- $(y - a) = m(x - b)$

Complete step-by-step answer:

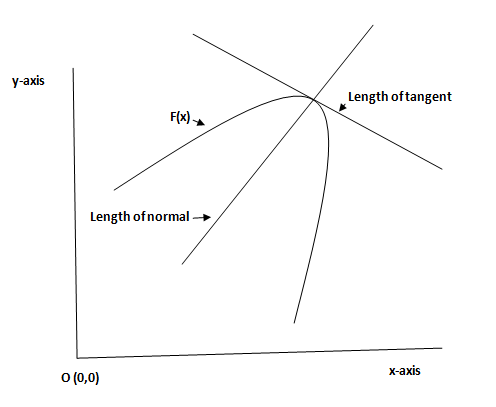
Given: Length of subtangent= length of subnormal

$$\Rightarrow y \times \dfrac{{dx}}{{dy}} = y \times \dfrac{{dy}}{{dx}} \\\ \Rightarrow {\left( {\dfrac{{dy}}{{dx}}} \right)^2} = 1 \\\ \Rightarrow \dfrac{{dy}}{{dx}} = \pm 1 \\\$$

Now, Equation of tangent passing through point (3,4) and having slope 1 is given as:

$$\Rightarrow (y - a) = m(x - b) \\\ \Rightarrow (y - 4) = 1(x - 3) \\\ \Rightarrow y = x + 1 \\\$$

So, the coordinates of A and B are (-1,0) and (0,1) respectively.
Area of $\triangle OAB$is given as:

$$\Rightarrow \dfrac{1}{2} \times OA \times OB \\\ \Rightarrow \dfrac{1}{2} \times 1 \times 1......(O = origin) \\\ \Rightarrow \dfrac{1}{2}sq.units \\\$$

Similarly, equation of tangent passing through point (3,4) and having slope 1 is given as:

$$\Rightarrow (y - a) = m(x - b) \\\ \Rightarrow (y - 4) = ( - 1)(x - 3) \\\ \Rightarrow y - 4 = 3 - x \\\ \Rightarrow y + x = 7 \\\$$

So, the coordinates of A and B are (7,0) and (0,7) respectively.
Area of $\triangle OAB$is given as:

$$\Rightarrow \dfrac{1}{2} \times OA \times OB \\\ \Rightarrow \dfrac{1}{2} \times 7 \times 7......(O = origin) \\\ \Rightarrow \dfrac{{49}}{2}sq.units \\\$$

So, the maximum area of $\triangle OAB$ is $\dfrac{{49}}{2}sq.units$.

Note: In above question we have given that the tangent meets coordinate axes means it will meet at abscissa and ordinate axes. The above coordinates can be found by putting once x=0 and then y=0.