Question

If the length of shadow and the height of tower are in the same ratio 1:1, then find the angle of elevation.

Answer 1

Let AB be the height of the tower and let BC be the length of the shadow of the tower, and $\theta$ be the angle of elevation. Next, write the given ratio as $\tan \theta$, where $\tan \theta$ is the ratio of perpendicular to base. Then, determine the value of angle for which $\tan \theta = 1$.

Complete step-by-step answer:
We are given that the ratio of length of shadow and the height of the tower is 1:1.

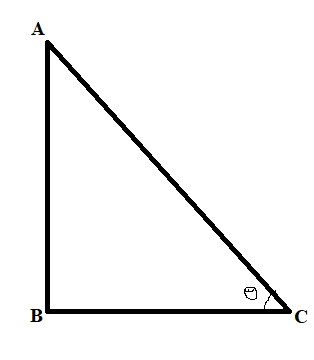
Let AB be the height of the tower and let BC be the length of the shadow of the tower as shown in the figure.
Let $\theta$ be the angle of elevation.
We have to find the value of $\theta$, when AB:BC=1:1
Here, in the triangle ABC, AB is the perpendicular and BC is the base.
The ratio $\dfrac{{AB}}{{BC}}$ give us the value of $\tan \theta$, as $\tan \theta$ is the ratio of perpendicular to base.
Hence,
$\tan \theta = \dfrac{{AB}}{{BC}} \\\ \Rightarrow \tan \theta = \dfrac{1}{1} \\\ \Rightarrow \tan \theta = 1 \\\$
Since, $\tan {45^ \circ } = 1$, therefore, the value of $\theta$ for the above equation is ${45^ \circ }$.
Thus, the required angle of elevation is ${45^ \circ }$.
Note: The angle made from the point of observation to the object is known as angle of elevation. We can also call this an upward angle from the horizontal line. Also, the student must know the trigonometric ratios, and the values of trigonometric ratios at different angles.