Question

If the inclination of line $\left( {2 - k} \right)x - \left( {1 - k} \right)y + \left( {5 - 2k} \right) = 0$ is $\dfrac{{3\pi }}{4}$ , then the value of k is
A. $\dfrac{5}{2}$
B. $\dfrac{-3}{2}$
C. $\dfrac{2}{3}$
D. $\dfrac{3}{2}$

Answer 1

Hint : The angle inclination of a line is the angle formed by the intersection of the line and X- axis. Find the slope of the line using a tangent of angle. Then find the slope of the line in terms of coefficients of $x$ and $y$ . Both the slopes must be the same. Use this to find the value of $k$ .

Complete step by step solution:
It is given that the inclination of line
$L \equiv \left( {2 - k} \right)x - \left( {1 - k} \right)y + \left( {5 - 2k} \right) = 0$ is $\dfrac{{3\pi }}{4}$

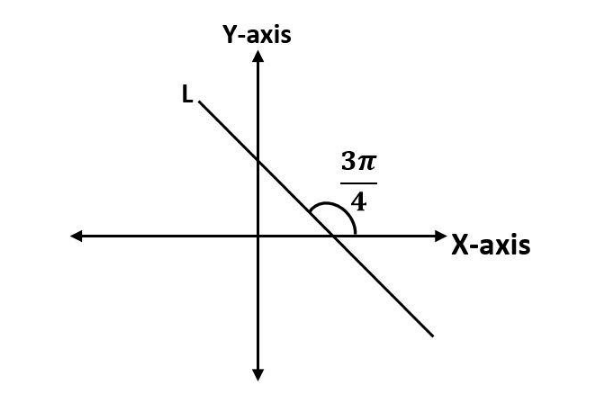
Let the slope of the given line $= m$
We know that, The slope of line $= \tan \theta$
$\therefore m = \tan \theta$
Put the value of $\theta$ in above equation,
We get, $m = \tan \dfrac{{3\pi }}{4} = - 1$
$- 1 = \dfrac{{k - 2}}{{k - 1}}$ . . . . $\left( {\tan \theta = \left| {\dfrac{y}{x}} \right|} \right)$
$\Rightarrow k - 1 = 2 - k$ . . . . (By cross multiplication)
$\Rightarrow k = \dfrac{3}{2}$ . . . . (On simplifying the above equation)
Therefore, from the above explanation, the correct option is (D) $\dfrac{3}{2}$ .
So, the correct answer is “Option D”.

Note : Inclination is the angle between two lines or planes where it intersects each other; the inclination of one line to another is measured in degrees or radians. The slope of the line using tangent of an angle is equal to the slope of the line using the coefficients of $x$ and $y$ , because both of them represent the slope of the same line.