Question

If the image of the point $(-3,k)$in the line $2x-y+6=0$is the point $(1,5)$then find the value of $k$.

Answer 1

- Hint: In this question first draw the figure. Use the property of reflection as image and object distance are at equal distance from the mirror. Also take distance as perpendicular distance. Then find the point of intersection of mirror line and line perpendicular to it and passes through. This gives a coordinate which is the mid-point of point P and image point. Then apply the midpoint formula to find the midpoint (-3, k) and (1,5). Suppose this point is $(\alpha ,\beta )$. This point lies on the line $2x-y+6=0$. Now put the value of $(\alpha ,\beta )$to get the value of k.

Complete step-by-step solution -
In this question the straight line $2x-y+6=0$play the role of mirror with respect to which we have the reflection of point (-3, k) is the point (1,5)
suppose AB is the line of mirror, so equation of mirror is
$2x-y+6=0$------------------------------(1)
Let$P(-3,k)$ be the point whose reflection is $Q(1,5)$.
Now we draw the figure.

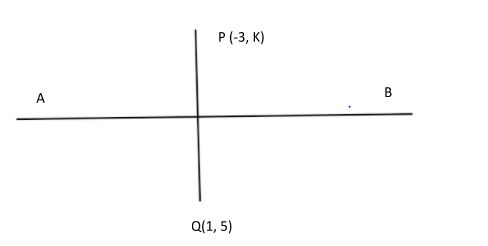
So, we can say that
$PQ\bot AB\text{ and PL=LQ}$as we know that image distance is equal to object distance
Here L is the foot of perpendicular from point P to Line AB.
Now since PL is perpendicular to the line (1) and passes through point $L(\alpha ,\beta )$.
As per the law of reflection the point $L(\alpha ,\beta )$be the midpoint of PQ, so we can write
$\alpha =\dfrac{-3+1}{2}$ and $\beta =\dfrac{k+5}{2}$
Here we use the midpoint formula. If $p({{x}_{1,}}{{y}_{1}})\text{ and }q({{x}_{2,}}{{y}_{2}})$be any two point then the midpoint is given by $M\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$
As the point $(\alpha ,\beta )$lies on the mirror line that is $2x-y+6=0$
Hence the point must satisfy the equation (1)
So, we can write
$2\alpha -\beta +6=0$
Now substituting the value of $\alpha$and$\beta$we can write
$\begin{aligned} & 2\left( \dfrac{-3+1}{2} \right)-\left( \dfrac{k+5}{2} \right)+6=0 \\\ & \Rightarrow \dfrac{2(-2)-(k+5)+12}{2}=0 \\\ & \Rightarrow -4-k-5+12=0 \\\ & \Rightarrow k=9-12 \\\ & \Rightarrow k=-3 \\\ \end{aligned}$
Hence, we get the value ok k=-3

Note: The given question can be solved by using the formula below directly
The image of a point $({{x}_{1}},{{y}_{1}})$with respect to the line mirror $ax+by+c=0$be $Q(x,y)$is given by$\dfrac{x-{{x}_{1}}}{a}=\dfrac{y-{{y}_{1}}}{b}=-\dfrac{2(a{{x}_{1}}+b{{y}_{1}}+c)}{{{a}^{2}}+{{b}^{2}}}$
In multiple choice questions we use the above formula in order to get the result fast.