Question

If the image of the point (2, 3) in the line $x+2y=6$ lies on the circle $\left(x-\frac{1}{5}\right)^2 + \left(y+\frac{3}{5}\right)^2 = r^2$, then $r^2$ is equal to:

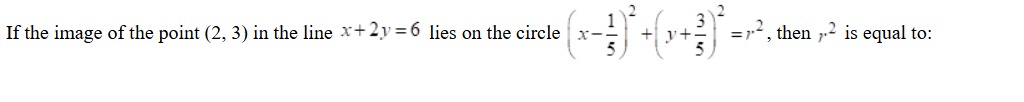
Answer 1

5

Answer 2

1. Reflect (2,3) across the line $x + 2y = 6$:

   • Write the line as $x + 2y - 6 = 0$ (here, $A = 1$, $B = 2$, $C = -6$).
   • The reflection formula for a point $P=(x_1, y_1)$ is: $$P' = \left( x_1 - \frac{2A(Ax_1+By_1+C)}{A^2+B^2},\, y_1 - \frac{2B(Ax_1+By_1+C)}{A^2+B^2} \right)$$
   • For $P=(2,3)$: $$Ax_1+By_1+C = 1\cdot2 + 2\cdot3 - 6 = 2+6-6 = 2,$$ $$A^2+B^2 = 1^2+2^2 = 5.$$
   • Thus, $$P' = \left( 2 - \frac{2\cdot1 \cdot 2}{5},\, 3 - \frac{2\cdot2 \cdot 2}{5} \right) = \left(2-\frac{4}{5},\, 3-\frac{8}{5}\right) = \left(\frac{6}{5},\, \frac{7}{5}\right).$$

2. Find $r^2$ such that $P'$ lies on the circle

   $$\left(x-\frac{1}{5}\right)^2 + \left(y+\frac{3}{5}\right)^2 = r^2.$$

   Substitute $x=\frac{6}{5}$ and $y=\frac{7}{5}$:

   $$\left(\frac{6}{5}-\frac{1}{5}\right)^2 + \left(\frac{7}{5}+\frac{3}{5}\right)^2 = \left(\frac{5}{5}\right)^2 + \left(\frac{10}{5}\right)^2 = 1^2 + 2^2 = 1 + 4 = 5.$$

   Hence, $r^2 = 5$.