Solveeit Logo
Login

Question

Question: If the high resistance voltmeter V shows a reading of \( 18{\text{V}} \) when the switch S is closed...

If the high resistance voltmeter V shows a reading of 18V18{\text{V}} when the switch S is closed, then the emf of the cell E must be

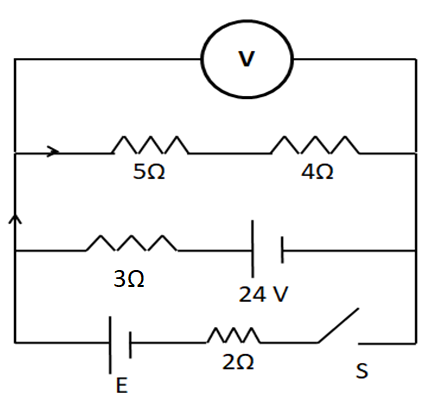
(A) 42V{\text{42V}}
(B) 6V{\text{6V}}
(C) 24V{\text{24V}}
(D) 18V18{\text{V}}

Explanation

Solution

Hint
To solve this question, we have to determine the currents in the different branches of the circuit by applying KVL and KCL. Then, with the help of these current values, we can find out the required emf.

Complete step by step answer
As the resistance of the voltmeter is high, no current will pass through it. So for the circuit analysis, we take it out of the circuit. On closing the switch S, the circuit looks like

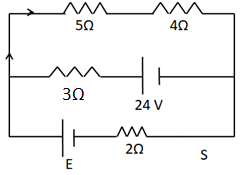
Now, we can see that the 5Ω5\Omega and the 4Ω4\Omega resistances are in series. So, their equivalent resistance is
R=5+4=9ΩR = 5 + 4 = 9\Omega. So the above circuit reduces to

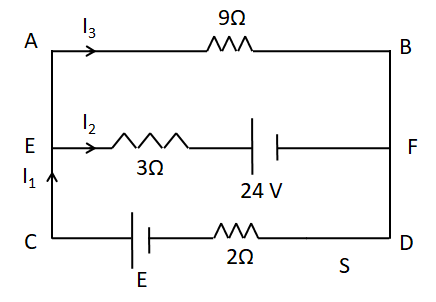
Since the voltmeter shows a reading of 18V18{\text{V}} so the potential difference between the points A and B is Vab=18V{V_{ab}} = 18{\text{V}}
From the above circuit diagram
⇒Vab=9I3\Rightarrow {V_{ab}} = 9{I_3}
⇒18=9I3\Rightarrow 18 = 9{I_3}
Dividing by 99 we get
⇒I3=2A\Rightarrow {I_3} = 2{\text{A}} …..(1)
Applying KVL in the loop EFBA
⇒3I2+24−9I3=0\Rightarrow 3{I_2} + 24 - 9{I_3} = 0
Substituting from (1)
⇒3I2+24−9(2)=0\Rightarrow 3{I_2} + 24 - 9\left( 2 \right) = 0
⇒3I2=−6\Rightarrow 3{I_2} = - 6
Dividing by 33 we get
⇒I2=−2A\Rightarrow {I_2} = - 2{\text{A}}
Applying KCL, we have
⇒I1=I2+I3\Rightarrow {I_1} = {I_2} + {I_3}
⇒I1=−2+2=0A\Rightarrow {I_1} = - 2 + 2 = 0{\text{A}} …...(2)
Now, applying KVL in the loop ABDC, we have
⇒9I3+2I1−E=0\Rightarrow 9{I_3} + 2{I_1} - E = 0
From (1) and (2)
⇒9(2)+2(0)−E=0\Rightarrow 9(2) + 2\left( 0 \right) - E = 0
⇒E=18V\Rightarrow E = 18{\text{V}}
So the emf of cell E is equal to 18V18{\text{V}}
Hence, the correct answer is option (D).

Note
The same question can be attempted very easily without entirely depending upon KVL and KCL. We can calculate the net emf and net resistance of the bottommost two branches, thereby reducing these two branches into a single branch. Then using the value of the reading of the voltmeter and applying the KVL, we can determine the emf of the unknown cell. Using this method will reduce the chances of committing the calculation mistakes.