Question
Question: If the height of a pole is \(2\sqrt{3}\) metres and the length of its shadow is \(2\) metres, find t...
If the height of a pole is 23 metres and the length of its shadow is 2 metres, find the angle of elevation of the sun.
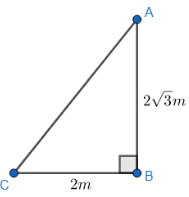
Solution
We know that the tangent of any angle is defined as tanθ=BasePerpendicular. So, if ∠BCA=θ, then we can write tanθ=BCAB. Hence by putting the values of AB and BC, and using the fact that tanθ=3, we can easily find the angle of elevation of the sun.
Complete step by step solution:
In the question, we are given that height of pole, AB = 23 metres,
and the length of its shadow, CB = 2 metres.
It is clear that the pole AB is standing vertically at the point B, on the surface of the ground. We also know that CB is the shadow of the pole AB, with point C being the shadow of point A.
So, we can say that ∠BCA is the angle of elevation of the sun.
Let us assume ∠BCA=θ.
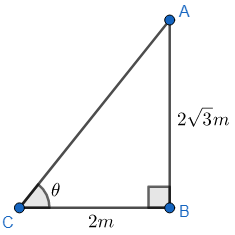
We can see that the triangle ABC is a right angled triangle, and thus we can use the trigonometric identities.
We know that the value of tangent of an angle is the ratio of perpendicular and the base. Mathematically, tanθ=BasePerpendicular.
So, in triangle ABC, we can write tanθ=BCAB.
Let us now substitute the values of AB and BC in the above equation. We get
tanθ=223
On simplification, we can write tanθ=3.
Thus, we get
θ=tan−13
Hence, we get that θ=60∘.
Thus, the angle of elevation of the sun is 60∘.
Note:
We must note that the value of tan−13 can either be 60∘ or 240∘. But, we know that any internal angle of a triangle can never be equal to 240∘, because the sum of all internal angles is 180∘. Thus, we can neglect the value 240∘.
