Question
Question: If the ground is sufficiently rough to ensure rolling, what is the kinetic energy of the body now in...
If the ground is sufficiently rough to ensure rolling, what is the kinetic energy of the body now in the given time interval of 2s?
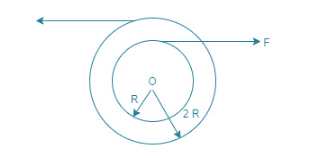
Solution
The rolling motion is one of the most common motions observed in daily life. For any disc to roll without slipping, the essential condition is
Vcm=Rω
Vcm =Translational velocity of disc
ω= Velocity of center of mass
R = Radius
Kinetic energy of rolling motion
K=KT+KR
KT =translational K.E
KR =Rotational K.E
KT=21 mv2cm
KR=21Iω2
Total energy will become
∴ K=21mvcm2+21Iω2
To solve this type of problem, keep in mind that it contains both kinetic energies. Therefore we will find out total kinetic energy. To find kinetic energy, we should have a value of translational velocity and angular velocity. To find out the value of velocities we will use the equation of motion. An equation of motion acceleration is also present. So, to find out the value of acceleration we will use Newton’s law of motion.
Complete step by step solution
We know that K.E of rolling motion is given by:
K=21mvcm2+21Iω2
Vcm=Rω
To find out Vcm and we will use equation of motion
V=u+at
In case of V and In case of ω
Vf=Vi+a t ….. (A) wf=wi+a t …. (B)
We know that
F=ma
a1=mf (Translational motion)................. (1)
And a2=IFR−f(2R) (rotational motion)................(2)
In the above expression, it is a moment of inertia.
For pure rolling a1=a2R
∴ mf=(IFR−f(2R))
Now, we will find moment of inertia by using following equation:
I=21 mr2 =21×2×(2)2 =4
Given values: f=10 R=1, I=4, m=2
⇒mf=(410×1−2f)
⇒2f=410−2f
⇒(f)(4)=2(10−2f)
⇒4f=20−4f
⇒4f+4f=20⇒8f=20⇒f=820=2.5N
And
a=mf
⇒a=22.5⇒1.25m/s2
In case of rotational motion
a2=IFR−f(2R)
Putting all values
⇒410×1−(2⋅5)(2)⇒45s−2
Now putting all values in (A) and (B)
Vf=Vi+a t wf=wi+a t
⇒0+(1⋅25)×(2) ⇒0×45×2
Vf=2⋅5 m/s wf=2⋅5 m/s−1
Now, use
K.E=21mv2+21 Iw2⇒21×2×(2⋅5)2+21×4×(2⋅5)2⇒18⋅75 J
Therefore, kinetic energy is 18.75J.
Note
We have laws of rotational motion. While solving problems regarding rotational motion use them. Keep in mind that when a body rolls on the ground it contains both kinetic energy that is total kinetic energy is the sum of kinetic energy of translational motion of center of mass and kinetic energy of rotational motion about center of mass.
